
1、下面各组函数中为相同函数的是 ( )
A.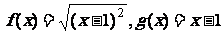 ,
,
B.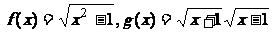
C.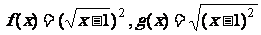
D.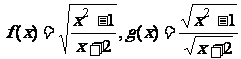
3、求解含参数的定义域问题及恒成立问题。
同步练习 2.2 函数的定义域
[选择题]
2、复合函数的定义域及求法:
1、函数定义域的求法:
[例1]求下列函数的定义域:
①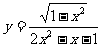 ②
②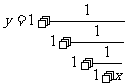
③y=lg(ax-2·3x)(a>0且a≠1)
解:①
②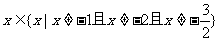
③
∵ax-2·3x>0 ∴( 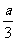 )x>2
)x>2
当a>3时,此函数的定义域为(log 2,+∞)
2,+∞)
当0<a<3且a≠1时,函数定义域为(-∞,log 2)
2)
当a=3时,函数无意义。
方法提炼:已知函数式求定义域--
[例2]已知 的定义域是[-1,3]
的定义域是[-1,3]
(1)求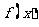 定义域;(2)求
定义域;(2)求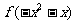 的定义域。
的定义域。
解(1)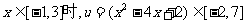
∴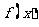 定义域为[-2,7]。
定义域为[-2,7]。
(2)由
∴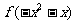 的定义域为[-2,1]。
的定义域为[-2,1]。
方法提炼:复合函数定义域的求法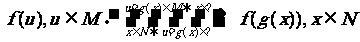
[例3]如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数 的解析式、定义域和最大值.
的解析式、定义域和最大值.
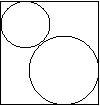 解:设另一个圆的半径为y,则
解:设另一个圆的半径为y,则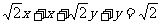
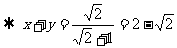 ,
, 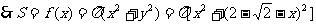

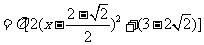 ,
,
∵当一个圆为正方形内切圆时半径最大,而另一圆半径最小,∴函数的定义域为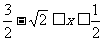 (注意定义域为闭区间)
(注意定义域为闭区间) 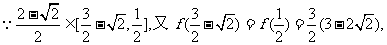
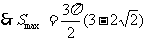 ,
,
[例4]设函数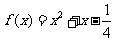 .
.
(Ⅰ)若定义域限制为[0,3],求f(x)的值域;
(Ⅱ)若定义域限制为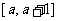 时,
时,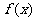 的值域为
的值域为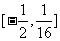 ,求a的值.
,求a的值.
解: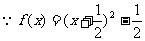 ,∴对称轴为
,∴对称轴为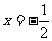 ,
,
(Ⅰ)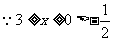 ,∴
,∴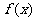 的值域为
的值域为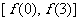 ,即
,即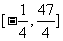 ;
;
(Ⅱ)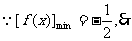 对称轴
对称轴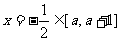 ,
,
 , ∵区间
, ∵区间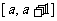 的中点为
的中点为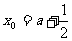 ,
,
(1)当 时,
时,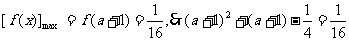 ,
,
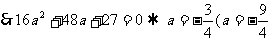 不合);
不合);
(2)当 时,
时,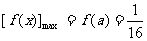 ,
,
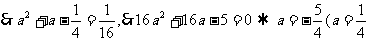 不合);
不合);
综上,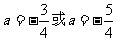 .
.
[研讨.欣赏]设f(x)=lg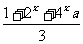 ,如果当x∈(-∞,1]时f(x)有意义,求实数a的取值范围。
,如果当x∈(-∞,1]时f(x)有意义,求实数a的取值范围。
思路点拔:当x∈(-∞,1]时f(x)有意义,转化为1+2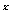 +4
+4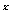 a>0在x∈(-∞,1]上恒成立问题,即 (
a>0在x∈(-∞,1]上恒成立问题,即 (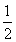 )
)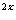 +(
+(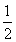 )
)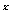 +a>0在x∈(-∞,1]上恒成立。
+a>0在x∈(-∞,1]上恒成立。
解:由题设可知,不等式1+2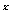 +4
+4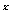 a>0在x∈(-∞,1]上恒成立,
a>0在x∈(-∞,1]上恒成立,
即:(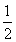 )
)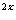 +(
+(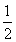 )
)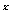 +a>0在x∈(-∞,1]上恒成立。
+a>0在x∈(-∞,1]上恒成立。
设t=(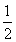 )
)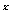 , 则t≥
, 则t≥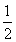 , 又设g(t)=t
, 又设g(t)=t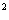 +t+a,其对称轴为t=-
+t+a,其对称轴为t=-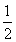
∴ t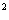 +t+a=0在[
+t+a=0在[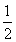 ,+∞)上无实根, 即 g(
,+∞)上无实根, 即 g(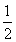 )=(
)=(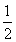 )
)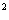 +
+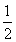 +a>0,得a>-
+a>0,得a>-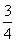
所以a的取值范围是a>-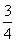 。
。
6.已知函数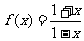 的定义域为M,f[f(x)]的定义域为N,则M∩N= .
的定义域为M,f[f(x)]的定义域为N,则M∩N= .
简答: 1-3、ABB;4. [-5,-2]∪[1,4];5.(-a,1+a);6.{x|x≠0且x≠1}
5.如果f(x)的定义域为(0,1), ,那么函数g(x)=f(x+a)+f(x-a)的定义域为
.
,那么函数g(x)=f(x+a)+f(x-a)的定义域为
.
4.已知f(x)的定义域为[0,1],则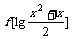 的定义域为 .
的定义域为 .
3.已知函数f(x)= 的定义域是R,则实数a的取值范围是 ( )
的定义域是R,则实数a的取值范围是 ( )
A.a>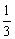 B.-12<a≤0
C.-12<a<0 D.a≤
B.-12<a≤0
C.-12<a<0 D.a≤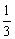
2.(2006湖北)设 ,则
,则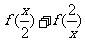 的定义域为( )
的定义域为( )
A.(-4,0)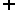 (0,4) B.(-4,-1)
(0,4) B.(-4,-1)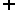 (1,4)
(1,4)
C.(-2,-1)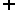 (1,2) D.(-4,-2)
(1,2) D.(-4,-2)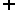 (2,4)
(2,4)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com