
10、已知函数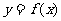 的定义域为[-1,1],求
的定义域为[-1,1],求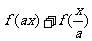 (a>0)的定义域。
(a>0)的定义域。
解:须使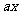 和
和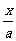 都有意义。
都有意义。
使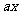 有意义则
有意义则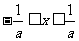 ;使
;使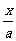 有意义则
有意义则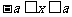 。
。
∴当 时,
时,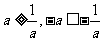 ,
,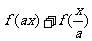 的定义域为
的定义域为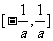 ;
;
∴当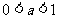 时,
时,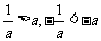 ,
,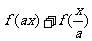 的定义域为
的定义域为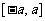 ;
;
[探索题] 某地为促进淡水鱼养殖业的发展,将价格控制在适当范围内,决定对淡水鱼养值提供政府补贴.设淡水鱼的市场价格为x元/千克,政府补贴为t元/千克.根据市场调查,当8≤x≤14时,淡水鱼的市场日供应量P千克与市场日需求量Q千克近似地满足关系:
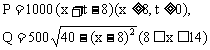
当P=Q时市场价格称为市场平衡价格.
(1)将市场平衡价格表示为政府补贴的函数,并求出函数的定义域;
(2)为使市场平衡价格不高于每千克10元,政府补贴至少为每千克多少元?
解:(1)依题设有
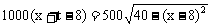
化简得 5x2+(8t-80)x+(4t2-64t+280)=0.
当判别式△=800-16t2≥0时,
可得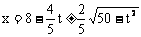
由△≥0,t≥0,8≤x≤14,得不等式组:
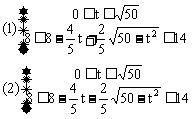
解不等式组①,得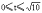 ,不等式组②无解.故所求的函数关系式为
,不等式组②无解.故所求的函数关系式为
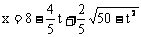
函数的定义域为[0,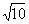 ]
]
(2)为使x≤10,应有
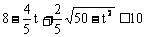
化简得t2+4t-5≥0.
解得t≥1或t≤-5,由t≥0知t≥1.从而政府补贴至少为每千克1元.
9、已知函数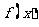 定义域为(0,2),求下列函数的定义域:
定义域为(0,2),求下列函数的定义域:
(1)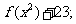 (2)
(2) 
分析:x的函数f(x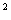 )是由u=x
)是由u=x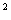 与f(u)这两个函数复合而成的复合函数,其中x是自变量,u是中间变量.由于f(x),f(u)是同一个函数,故(1)为已知0<u<2,即0<x
与f(u)这两个函数复合而成的复合函数,其中x是自变量,u是中间变量.由于f(x),f(u)是同一个函数,故(1)为已知0<u<2,即0<x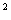 <2.求x的取值范围.
<2.求x的取值范围.
解:(1)由0<x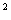 <2, 得
<2, 得
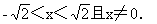
所以 f(x2)的定义域为
(2)由(1)解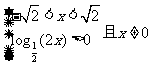 ,
,
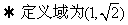
8、已知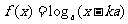 ,
,

 的定义域。
的定义域。
解: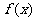 的定义域(ka,+∞),
的定义域(ka,+∞),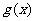 的定义域(-∞-a)∪(a,∞)
的定义域(-∞-a)∪(a,∞)
∴当k>1时,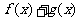 的定义域为(ka,+∞);
的定义域为(ka,+∞);
当-1≤k≤1时,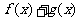 的定义域为(a,+∞);
的定义域为(a,+∞);
当k<-1时,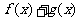 的定义域为(ka,-a)∪(a,+∞).
的定义域为(ka,-a)∪(a,+∞).
7、 求下列函数的定义域:
(1) 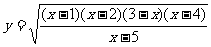
(2) y=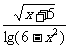 lg(6-x2)
lg(6-x2)
(3)y=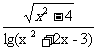
解:(1) 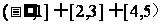
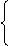
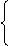 x+5>0
x≥-5
x+5>0
x≥-5
(2)∵ 6-x2>0 ∴ -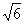 <x<
<x<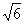
6-x2≠1
x≠±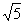
∴-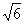 <x<
<x<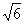 且x≠±
且x≠±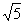
所求定义域为(-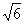 ,-
,-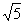 )∪(-
)∪(-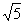 ,
,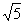 )∪(
)∪(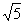 ,
,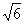 )
)
(3)要使函数有意义,必须且只需
 x2-4≥0
x≤-2或x≥2
x2-4≥0
x≤-2或x≥2
x2+2x-3>0 即 x<-3或x>1
lg(x2+2x-3)≠0 x≠-1±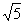
∴x<-3或x≥2,且x≠-1-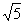
故函数定义域为{x|x<-3或x≥2,且x≠-1-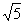 }
}
6、[a,-a], [-4,-2]∪[2,4]
[解答题]
6、已知函数f (x)的定义域为[a,b],其中0<-a<b,则F (x)=f (x)-f (-x)的定义域为___________,若y=log2(x2-2)的值域为[1,log214],则其定义域为_____________.
答案提示:1-4、DBCD;5、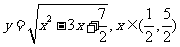
5、在△ABC中,BC=2,AB+AC=3.中线AD的长为y,若以AB的长为x,则y与x的函数关系和定义域是
4.若函数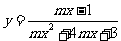 的定义域为R,则实数m的取值范围是( )
的定义域为R,则实数m的取值范围是( )
A.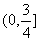 B.
B.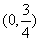 C.
C.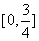 D.
D.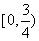
[填空题]
3、若函数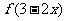 的定义域为[-1,2],则函数
的定义域为[-1,2],则函数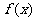 的定义域是( )
的定义域是( )
A.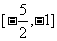 B.[-1,2] C.[-1,5]
D.
B.[-1,2] C.[-1,5]
D.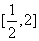
2、(2006广东) 函数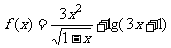 的定义域是( )
的定义域是( )
A、 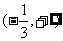 B、
B、 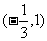 C、
C、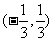 D、
D、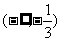
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com