
6.关于氯化铁水解的说法错误的是 ( )
A.水解达到平衡(不饱和)时,无论加氯化铁饱和溶液还是加水稀释,平衡均向正方向移动
B.浓度为5 mol/L和0.5 mol/L的两种FeCl3溶液,其他条件相同时,Fe3+的水解程度前者比后者小
C.有50℃和20℃的同浓度的FeCl3溶液,其他条件相同时,Fe3+的水解程度前者比后者小
D.为抑制Fe3+水解,较好地保存FeCl3溶液,应加少量盐酸
解析:增大FeCl3的浓度,平衡正向移动,但水解程度减小,加水稀释,平衡正向移动,水解程度增大,A、B均正确;水解是吸热反应,温度升高,水解程度增大,C错误;Fe3+水解显酸性,增大H+浓度可抑制Fe3+的水解,D正确.
答案:C
5.已知乙酸(HA)的酸性比甲酸(HB)弱,在物质的量浓度均为0.1 mol/L的NaA和NaB混合溶液中,下列排序正确的是 ( )
A.c(OH-)>c(HA)>c(HB)>c(H+)
B.c(OH-)>c(A-)>c(B-)>c(H+)
C.c(OH-)>c(B-)>c(A-)>c(H+)
D.c(OH-)>c(HB)>c(HA)>c(H+)
解析:酸越弱,对应的盐的水解程度越大,同浓度的NaA和NaB的溶液中,前者水解程度更大,因此HA的浓度更大一些,D项错误;盐的水解程度很弱,故c(OH-)不可能大于c(A-)和c(B-),故B、C错误.
答案:A
4.向三份0.1 mol/L CH3COONa溶液中分别加入少量NH4NO3、Na2SO3、FeCl3固体(忽略溶液体积变化),则CH3COO-浓度的变化依次为 ( )
A.减小、增大、减小 B.增大、减小、减小
C.减小、增大、增大 D.增大、减小、增大
解析:在CH3COONa溶液中存在平衡:CH3COO-+H2O CH3COOH+OH-.加入NH4NO3固体促进了CH3COO-水解,平衡右移,CH3COO-浓度减小;加入Na2SO3抑制了CH3COO-水解,平衡左移,CH3COO-浓度增大;加入FeCl3促进了CH3COO-的水解,平衡右移,CH3COO-浓度减小.
CH3COOH+OH-.加入NH4NO3固体促进了CH3COO-水解,平衡右移,CH3COO-浓度减小;加入Na2SO3抑制了CH3COO-水解,平衡左移,CH3COO-浓度增大;加入FeCl3促进了CH3COO-的水解,平衡右移,CH3COO-浓度减小.
答案:A
3.用一价离子组成的四种盐溶液:AC、BD、AD、BC,其物质的量浓度分别为1 mol/L,在室温下前两种溶液的pH=7,第三种溶液的pH>7,最后一种溶液pH<7,则正确的是 ( )
|
|
A |
B |
C |
D |
|
碱性 |
AOH>BOH |
AOH<BOH |
AOH>BOH |
AOH<BOH |
|
酸性 |
HC>HD |
HC>HD |
HC<HD |
HC<HD |
解析:强酸强碱盐不水解,溶液呈中性;强酸弱碱盐,溶液呈酸性;强碱弱酸盐,溶液呈碱性;弱酸弱碱盐,溶液可能呈中性、酸性,也可能呈碱性.根据题意,AOH为强碱,BOH为弱碱;HC为强酸,HD为弱酸.
答案:A
2.下列有关问题,与盐的水解有关的是 ( )
①NH4Cl与ZnCl2溶液可作焊接金属中的除锈剂
②用NaHCO3与Al2(SO4)3两种溶液可作泡沫灭火剂
③草木灰与铵态氮肥不能混合施用
④实验室盛放碳酸钠溶液的试剂瓶不能用磨口玻璃塞
⑤加热蒸干AlCl3溶液得到Al(OH)3固体
A.①②③ B.②③④
C.①④⑤ D.①②③④⑤
解析:①中NH4Cl与ZnCl2溶液水解均显酸性,可除去金属表面的锈;②HCO与Al3+水解相互促进,产生二氧化碳,可作灭火剂;③草木灰的主要成分碳酸钾水解显碱性,而铵态氮肥水解显酸性,因而不能混合施用;④碳酸钠溶液水解显碱性,而磨口玻璃塞中的二氧化硅会与碱反应生成硅酸钠将瓶塞与瓶口黏结,因此盛放碳酸钠的试剂瓶应用橡胶塞;⑤AlCl3溶液中存在水解平衡:AlCl3+3H2O Al(OH)3+3HCl,加热时,HCl挥发使平衡不断右移,最终得到Al(OH)3固体.
Al(OH)3+3HCl,加热时,HCl挥发使平衡不断右移,最终得到Al(OH)3固体.
答案:D
1.(2009·天津高考)25℃时,浓度均为0.2 mol/L的NaHCO3和Na2CO3溶液中,下列
判断不正确的是 ( )
A.均存在电离平衡和水解平衡
B.存在的粒子种类相同
C.c(OH-)前者大于后者
D.分别加入NaOH固体,恢复到原温度,c(CO)均增大
解析:A项,两种溶液中均存在着水的电离平衡,NaHCO3溶液中还存在:HCO H++CO及HCO+H2O
H++CO及HCO+H2O H2CO3+OH-,Na2CO3溶液中还存在有CO+H2O
H2CO3+OH-,Na2CO3溶液中还存在有CO+H2O HCO+OH-,故A正确.B项,两种溶液中均存在Na+、CO、HCO、H2CO3、OH-、H+、H2O,B正确.C项,浓度相同时,CO水解程度大于HCO,故Na2CO3溶液中c(OH-)要大,故C错.D项,NaHCO3溶液中加入NaOH固体:HCO+OH-===H2O+CO,c(CO)增大,Na2CO3溶液中加入NaOH,导致CO的水解平衡向左移动,c(CO)增大,故D正确.
HCO+OH-,故A正确.B项,两种溶液中均存在Na+、CO、HCO、H2CO3、OH-、H+、H2O,B正确.C项,浓度相同时,CO水解程度大于HCO,故Na2CO3溶液中c(OH-)要大,故C错.D项,NaHCO3溶液中加入NaOH固体:HCO+OH-===H2O+CO,c(CO)增大,Na2CO3溶液中加入NaOH,导致CO的水解平衡向左移动,c(CO)增大,故D正确.
答案:C
(三) 解答题
16、设集合A={(x,y)|y=ax+1},B={(x,y)|y=|x|},若A∩B是单元素集合,求a取值范围。
17、已知抛物线C:y=-x2+mx-1,点M(0,3),N(3,0),求抛物线C与线段MN有两个不同交点的充要条件。
18、设A={x|x2+px+q=0}≠φ,M={1,3,5,7,9},N={1,4,7,10},若A∩M=φ,A∩N=A,求p、q的值。
19、已知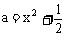 ,b=2-x,c=x2-x+1,用反证法证明:a、b、c中至少有一个不小于1。
,b=2-x,c=x2-x+1,用反证法证明:a、b、c中至少有一个不小于1。
(二) 填空题
11、已知M={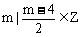 },N={x|
},N={x| ,则M∩N=__________。
,则M∩N=__________。
12、在100个学生中,有乒乓球爱好者60人,排球爱好者65人,则两者都爱好的人数最少是________人。
13、关于x的方程|x|-|x-1|=a有解的充要条件是________________。
14、命题“若ab=0,则a、b中至少有一个为零”的逆否命题为____________。
15、非空集合p满足下列两个条件:(1)p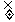 {1,2,3,4,5},(2)若元素a∈p,则6-a∈p,则集合p个数是__________。
{1,2,3,4,5},(2)若元素a∈p,则6-a∈p,则集合p个数是__________。
(一) 选择题
1、设M={x|x2+x+2=0},a=lg(lg10),则{a}与M的关系是
A、{a}=M B、M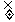 {a} C、{a}
{a} C、{a} M D、M
M D、M {a}
{a}
2、已知全集U=R,A={x|x-a|<2},B={x|x-1|≥3},且A∩B=φ,则a的取值范围是
A、 [0,2] B、(-2,2) C、(0,2] D、(0,2)
3、已知集合M={x|x=a2-3a+2,a∈R},N、{x|x=b2-b,b∈R},则M,N的关系是
A、 M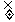 N B、M
N B、M N
C、M=N
D、不确定
N
C、M=N
D、不确定
4、设集合A={x|x∈Z且-10≤x≤-1},B={x|x∈Z,且|x|≤5},则A∪B中的元素个数是
A、11 B、10 C、16 D、15
5、集合M={1,2,3,4,5}的子集是
A、15 B、16 C、31 D、32
6、对于命题“正方形的四个内角相等”,下面判断正确的是
A、所给命题为假 B、它的逆否命题为真 C、它的逆命题为真 D、它的否命题为真
7、“α≠β”是cosα≠cosβ”的
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
8、集合A={x|x=3k-2,k∈Z},B={y|y=3+1,∈Z},S={y|y=6m+1,m∈Z}之间的关系是
A、S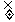 B
B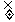 A B、S=B
A B、S=B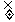 A C、S
A C、S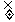 B=A D、S
B=A D、S B=A
B=A
9、方程mx2+2x+1=0至少有一个负根的充要条件是
A、0<m≤1或m<0 B、0<m≤1 C、m<1 D、m≤1
10、已知p:方程x2+ax+b=0有且仅有整数解,q:a,b是整数,则p是q的
A、充分不必要条件 B、必要不充分条件 C.充要条件 D、既不充分又不必要条件
例1、已知集合M={y|y=x2+1,x∈R},N={y|y=x+1,x∈R},求M∩N。
解题思路分析:
在集合运算之前,首先要识别集合,即认清集合中元素的特征。M、N均为数集,不能误认为是点集,从而解方程组。其次要化简集合,或者说使集合的特征明朗化。M={y|y=x2+1,x∈R}={y|y≥1},N={y|y=x+1,x∈R}={y|y∈R}
∴ M∩N=M={y|y≥1}
说明:实际上,从函数角度看,本题中的M,N分别是二次函数和一次函数的值域。一般地,集合{y|y=f(x),x∈A}应看成是函数y=f(x)的值域,通过求函数值域化简集合。此集合与集合{(x,y)|y=x2+1,x∈R}是有本质差异的,后者是点集,表示抛物线y=x2+1上的所有点,属于图形范畴。集合中元素特征与代表元素的字母无关,例{y|y≥1}={x|x≥1}。
例2、已知集合A={x|x2-3x+2=0},B+{x|x2-mx+2=0},且A∩B=B,求实数m范围。
解题思路分析:
化简条件得A={1,2},A∩B=B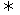 B
B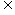 A
A
根据集合中元素个数集合B分类讨论,B=φ,B={1}或{2},B={1,2}
当B=φ时,△=m2-8<0
∴

当B={1}或{2}时,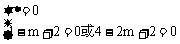 ,m无解
,m无解
当B={1,2}时,
∴ m=3
综上所述,m=3或
说明:分类讨论是中学数学的重要思想,全面地挖掘题中隐藏条件是解题素质的一个重要方面,如本题当B={1}或{2}时,不能遗漏△=0。
例3、用反证法证明:已知x、y∈R,x+y≥2,求 证x、y中至少有一个大于1。
解题思路分析:
假设x<1且y<1,由不等式同向相加的性质x+y<2与已知x+y≥2矛盾
∴ 假设不成立
∴ x、y中至少有一个大于1
说明;反证法的理论依据是:欲证“若p则q”为真,先证“若p则非q”为假,因在条件p下,q与非q是对立事件(不能同时成立,但必有一个成立),所以当“若p则非q”为假时,“若p则q”一定为真。
例4、若A是B的必要而不充分条件,C是B的充要条件,D是C的充分而不必要条件,判断D是A的什么条件。
解题思路分析:
利用“ ”、“
”、“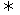 ”符号分析各命题之间的关系
”符号分析各命题之间的关系
D C
C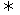 B
B A
A
∴ D A,D是A的充分不必要条件
A,D是A的充分不必要条件
说明:符号“ ”、“
”、“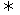 ”具有传递性,不过前者是单方向的,后者是双方向的。
”具有传递性,不过前者是单方向的,后者是双方向的。
例5、求直线:ax-y+b=0经过两直线1:2x-2y-3=0和2:3x-5y+1=0交点的充要条件。
解题思路分析:
从必要性着手,分充分性和必要性两方面证明。
由
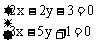 得1,2交点P(
得1,2交点P(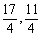 )
)
∵ 过点P
∴

∴ 17a+4b=11
充分性:设a,b满足17a+4b=11
∴
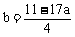
代入方程: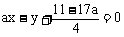
整理得:
此方程表明,直线恒过两直线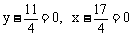 的交点(
的交点(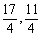 )
)
而此点为1与2的交点
∴ 充分性得证
∴ 综上所述,命题为真
说明:关于充要条件的证明,一般有两种方式,一种是利用“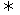 ”,双向传输,同时证明充分性及必要性;另一种是分别证明必要性及充分性,从必要性着手,再检验充分性。
”,双向传输,同时证明充分性及必要性;另一种是分别证明必要性及充分性,从必要性着手,再检验充分性。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com