1.子　 集

一般地，对于两个集合，如果A中任意一个元素都是B的元素，称集合A是集合B的子集，记作AÍB.读作“A包含于B”或“B包含A”.这时说集合A是集合B的子集.

注意：①区分∈；②也可用Ì.

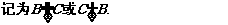这时, 我们说集合A是集合C的子集. 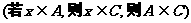而从B与C来看，显然B不包含于C. 　

2.过程与方法

①通过类比两个实数之间的大小关系，探究两个集合之间的关系；　　

②通过实例分析，获知两个集合间的包含与相等关系，然后给出定义.

教学重点与难点：

重点：子集的概念.

难点：元素与子集，即属于与包含之间的区别.

教学过程：

实数有相等关系，大小关系，类比实数之间的关系，集合之间是否具备类似的关系？

示例1：观察下面三个集合, 找出它们之间的关系:　

A＝{1，2，3}　 B＝{1，2，7}　 C＝{1，2，3，4，5}

1.知识与技能

①理解 集合的包含和相等的关系；　　 ②了解使用Venn图表示集合及其关系；

③掌握包含和相等有关术语、符号，并会使用它们表达集合之间的关系.

1.1.2 集合间的基本关系㈠

教学目标：

1.集合的定义　 2.集合元素的性质　 3.集合与元素的关系　 4.集合的表示　 5.集合的分类

课后作业　　 教科书12面习题1.1第3、4题

1.教科书5面练习第1、2题　　　　　 2.教科书11面习题1.1第1、2题

课堂小结

7.重要的数集:

N：自然数集(含0)　　 N+：正整数集(不含0)　　 Z：整数集

Q：有理数集　　　　　 R：实数集

例1若x∈R，则数集{1，x，x²}中元素x应满足什么条件.

解：∵x≠1且x²≠1且x²≠x，　 ∴ x≠1且x≠－1且x≠0.

例2设x∈R，y∈R，观察下面四个集合　　　

A＝{ y＝x²－1 }　 B＝{ x | y＝x²－1 }　 C＝{ y | y＝x²－1 }　 　D＝{ (x, y) | y＝x²－1 }

它们表示含义相同吗?

例3若方程x²－5x+6＝0和方程x²－x－2＝0的解为元素的集为M，则M中元素的个数为(　 C　 )

A.1　　　　 B.2　　　　　 C.3　　　　 D.4

例4已知集合A＝{x|ax²+4x+4＝0，x∈R，a∈R}只有一个元素，求a的值与这个元素.

解：当a＝0时，x＝－1. 当a≠0时，D＝16－4×4a＝0.　 a＝1. 　此时x＝－2.

∴a＝1时这个元素为－2.　 　∴a＝0时这个元素为－1.　

课堂练习

6.集合的分类：有限集、无限集.

问题2：我们看这样一个集合：{x|x²+x+1＝0}它有什么特征？

显然这个集合没有元素.我们把这样的集合叫做空集，记作Æ.

练习2：⑴ 0 　　Ï　 Æ　　 (填∈或Ï)　　 ⑵ { 0 } 　≠　 Æ　 (填＝或≠)

5.集合的表示方法:描述法、列举法、图表法

问题1：

用集合表示①x²－3＝0的解集;②所有大于0小于10的奇数;③不等式2x－1＞3的解.

4.集合元素的性质：

⑴ 确定性: 集合中的元素必须是确定的.例x∈A与xÏA必居其一.

⑵互异性: 集合的元素必须是互异不相同的.如: 方程 x²－2x+1＝0的解集为{1}而非{1, 1}

⑶无序性: 集合中的元素是无先后顺序的. 如：{1，2}，{2，1}为同一集合.

那么{(1，2)}，{(2，1)}是否为同一集合?