
例1 求下列函数的定义域:
①  ;②
;②  ;③
;③ 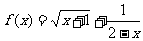 .
.
解:①∵x-2=0,即x=2时,分式 无意义,
无意义,
而 时,分式
时,分式 有意义,∴这个函数的定义域是
有意义,∴这个函数的定义域是 .
.
②∵3x+2<0,即x<-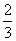 时,根式
时,根式 无意义,
无意义,
而 ,即
,即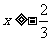 时,根式
时,根式 才有意义,
才有意义,
∴这个函数的定义域是{ |
|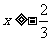 }.
}.
③∵当 ,即
,即 且
且 时,根式
时,根式 和分式
和分式 同时有意义,
同时有意义,
∴这个函数的定义域是{ |
| 且
且 }
}
另解:要使函数有意义,必须:  Þ
Þ 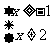
∴这个函数的定义域是: { |
| 且
且 }
}
例2 已知函数 =3
=3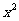 -5x+2,求f(3), f(-
-5x+2,求f(3), f(- ), f(a+1).
), f(a+1).
解:f(3)=3×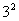 -5×3+2=14;
-5×3+2=14;
f(- )=3×(-
)=3×(- )
)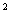 -5×(-
-5×(- )+2=8+5
)+2=8+5 ;
;
f(a+1)=3(a+1) 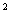 -5(a+1)+2=3a
-5(a+1)+2=3a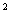 +a.
+a.
例3下列函数中哪个与函数 是同一个函数?
是同一个函数?
⑴ ;⑵
;⑵ ;⑶
;⑶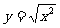
解:⑴ =
= (
( ),
), ,定义域不同且值域不同,不是;
,定义域不同且值域不同,不是;
⑵ =
= (
( ),
),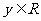 ,定义域值域都相同,是同一个函数;
,定义域值域都相同,是同一个函数;
⑶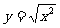 =|
=| |=
|=
 ,
, ;值域不同,不是同一个函数。
;值域不同,不是同一个函数。
例4 下列各组中的两个函数是否为相同的函数?
①

 (定义域不同)
(定义域不同)
②
 (定义域不同)
(定义域不同)
③
 (定义域、值域都不同)
(定义域、值域都不同)
3.二次函数
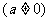 :定义域R
:定义域R
值域:当 时,
时, ;当
;当 时,
时,
2.反比例函
 :定义域
:定义域 , 值域
, 值域 ;
;
1.一次函数
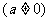 :定义域R, 值域R;
:定义域R, 值域R;
3.图象法:用图象表示两个变量之间的对应关系.
(4)已学函数的定义域和值域
2.列表法:列出表格来表示两个变量之间的对应关系.
(1)设A、B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f (x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数(function),记作y = f (x),x∈A.其中,x叫做自变量,x的取值范围A叫做函数的定义域(domain);与x的值相对应的y值叫做函数值。
(2)下列例1、例2、例3是否满足函数定义
例1 若物体以速度v作匀速直线运动,则物体通过的距离S与经过的时间t的关系是S = vt.例2 某水库的存水量Q与水深h(指最深处的水深)如下表:
|
水深h(米) |
0 |
5 |
10 |
15 |
20 |
25 |
|
存水量Q(立方) |
0 |
20 |
40 |
90 |
160 |
275 |
例3 设时间为t,气温为T(℃),自动测温仪测得某地某日从凌晨0点到半夜24点的温度曲线如下图.

分析:例1的对应法则f:t→s = Vt,定义域t∈[0, +∞).
例2的对应法则一个表格h→Q,定义域h∈{0, 5, 10, 15, 20, 25}.
例3的对应法则f:一条曲线,t∈[0,24]. 对任意t,过t作t轴的垂线与曲线交于一点P (t, T),即t→T. 通过三个实例反映函数的三种表示形式.
(2)函数的三要素: 对应法则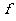 、定义域A、值域
、定义域A、值域
只有当这三要素完全相同时,两个函数才能称为同一函数。
关于函数值  ,例:
,例: =
=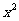 +3x+1 则 f(2)=
+3x+1 则 f(2)= +3×2+1=11
+3×2+1=11
注意:1°在 中
中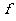 表示对应法则,不同的函数其含义不一样。
表示对应法则,不同的函数其含义不一样。
2° 不一定是解析式,有时可能是“列表”“图象”。
不一定是解析式,有时可能是“列表”“图象”。
3° 与
与 是不同的,前者为变数,后者为常数。
是不同的,前者为变数,后者为常数。
(3)表示函数的方法:
1.解析式:把常量和表示自变量的字母用一系列运算符号连接起来,得到的式子叫做解析式.
(1)函数的概念:(初中)在一个变化过程中有两个变量x和y,如果对于x的每一个值,y都有唯一的值与对应. 那么就说y是x的函数,其中x叫做自变量。
初中学过哪些函数?
正比例函数、反比例函数、一次函数、二次函数等。
示例分析
示例1:一枚炮弹发射后,经过26s落到地面击中目标. 炮弹的射高①为845m,且炮弹距地面的高度h (单位:m)随时间t (单位:s)变化的规律是h = 130t – 5t2.
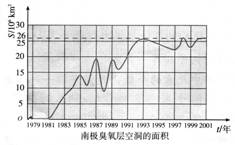 示例2:近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空沿问题. 下图中的曲线显示了南极上空臭氧层空洞的面积从1979-2001年的变化情况.
示例2:近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空沿问题. 下图中的曲线显示了南极上空臭氧层空洞的面积从1979-2001年的变化情况.
|
时间(年) |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
|
城镇居民家庭恩格尔系数(%) |
53.8 |
52.9 |
50.1 |
49.9 |
49.9 |
48.6 |
|
时间(年) |
1997 |
1998 |
1999 |
2000 |
2001 |
|
|
城镇居民家庭恩格尔系数(%) |
46.4 |
44.5 |
41.9 |
39.2 |
37.9 |
|
示例3 国际上常用恩格尔系数②反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高,下表中恩格尔系数随时间(年)变化的情况表明,“八五”计划以来,我国城镇居民的生活质量发生了显著变化.
“八五”计划以来我国城镇居民
恩格尔系数变化情况
3.课堂小结
1°能熟练求解一个给定集合的补集;
2°注意一以后些特殊结论在解题中的应用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com