
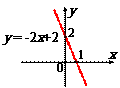
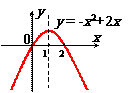
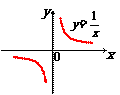
5.常见函数图像


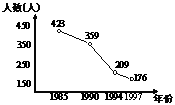
4. 长沙市耕地面积统计表
3. 长沙市日平均出生人数统计表
2. 长沙市高等学校在校学生数统计表
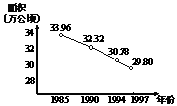
1. 长沙市年生产总值统计表
(2) 取元任意性,成象唯一性;
(3) A中元素不可剩,B中元素可剩;
(4) 多对一行,一对多不行;
(5) 映射具有方向性:f : A→B与f : B→A是不同的映射;
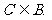 (6) 原象的集合为A, 象集
(6) 原象的集合为A, 象集
3、一一映射定义
若f是从集合A到B的映射,如果对集合A中的不同元素在集合B中都有不同的象,并且B中每一个元素在A中都有原象,这样的映射叫做从集合A到集合B的一一映射.
2.象与原象的定义:
给定一个集合A到B的映射,且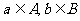 .若a与b对应,则把元素b叫做a在B中的象,而a叫做b的原象.如图(3)中, 30°是
.若a与b对应,则把元素b叫做a在B中的象,而a叫做b的原象.如图(3)中, 30°是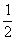 的原象,
的原象,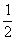 是30°的象,此时象集C=B,但在(4)中,
是30°的象,此时象集C=B,但在(4)中, .
.
例5.已知 ,
,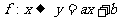 ,若1,8的原象相应的是3和10,
,若1,8的原象相应的是3和10,
求5在f下的象.
解:∵1,8的原象相应的是3和10
∴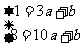 解得:
解得: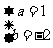
∴
∴5在f下的象是5-2=3.
例6.已知A={1,2,3},B={0,1},写出A到B的所有映射.
共8个映射.
例1 判断下列对应是否映射?有没有对应法则?
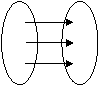


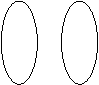
 a
e a e
a e
a
e a e
a e

 b
f b f
b f
b
f b f
b f

 c
g c g c
g
c
g c g c
g
d d
(是) (不是) (是)
1、3是映射,有对应法则,对应法则是用图形表示出来的
例2、下列各组映射是否为同一映射?
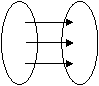

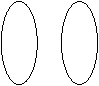


 a e
a
e
d e
a e
a
e
d e

 b
f
b
f
b
f
b
f
b
f
b
f
 c g
c
g
c g
c g
c
g
c g
 例3、下列对应关系(A到B)中,其中
例3、下列对应关系(A到B)中,其中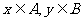 .
.

解:是映射的有(2)(4)(5).
例4、以下给出的对应是不是从集合A到B的映射?
(1)集合A = {P | P是数轴上的点},集合B = R,
对应关系f:数轴上的点与它所代表的实数对应;
(2)集合A = {P | P是平面直角坐标系中的点},集合B = {(x ,y) | x∈R,y∈R},
对应关系f:平面直角坐标系中的点与它的坐标对应;
(3)集合A = {x | x是三角形},集合B = {x | x是圆},
对应关系f:每一个三角形都对应它的内切圆;
(4)集合A = {x | x是新华中学的班级},集合B = {x | x是新华中学的学生},
对应关系f:每一个班级都对应班里的学生.
思考:如果从对应来说,什么样的对应才是一个映射?你能说出函数与映射之间的异同吗?
1)一对一,多对一是映射 但一对多显然不是映射
但一对多显然不是映射
2) 函数是一个特殊的映射;
3) 函数是非空数集A到非空数集B的映射,而对于映射, A和B不一定是数集;
3、映射三要素:集合A、B以及对应法则 ,缺一不可;
,缺一不可;
① 有序的:映射是有方向的,A到B的映射与B到A的映射往往不是同一个映射,
如:A到B是求平方,B到A则是开平方。
② 存在性:就是说对集合A中任何一个元素,集合B中都有元素和它对应。
③ 唯一性:对于集合A中的任何一个元素,集合B中都是唯一的元素和它对应。
④ 封闭性:“在集合B中”:也就是说A中元素的象必在集合B中.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com