
2、奇函数与偶函数图象的对称性:
如果一个函数是奇函数,则这个函数的图象以坐标原点为对称中心的中心对称图形. 反之,如果一个函数的图象是以坐标原点为对称中心的中心对称图形,则这个函数是奇函数.
如果一个函数是偶函数,则它的图形是以y轴为对称轴的轴对称图形;反之,如果一个函数的图象关于y轴对称,则这个函数是偶函数.
1、奇函数、偶函数的定义:
奇函数:设函数y = f (x)的定义域为D,如果对D内的任意一个x,都有f (–x) = – f (x),
则这个函数叫奇函数.
偶函数:设函数y = g (x)的定义域为D,如果对D内的任意一个x,都有g (– x) = g (x),
则这个函数叫做偶函数.
问题1:奇函数、偶函数的定义中有“任意”二字,说明函数的奇偶性是怎样的一个性质?与单调性有何区别?
强调定义中“任意”二字,说明函数的奇偶性在定义域上的一个整体性质,它不同于函数的单调性 .
问题2:–x与x在几何上有何关系?具有奇偶性的函数的定义域有何特征?
奇函数与偶函数的定义域的特征是关于原点对称.
问题3:结合函数f (x) =x3的图象回答以下问题:
(1)对于任意一个奇函数f (x),图象上的点P (x,f (x))关于原点对称点P′的坐标是什么?
点P′是否也在函数f (x)的图象上?由此可得到怎样的结论.
(2)如果一个函数的图象是以坐标原点为对称中心的中心对称图形,能否判断它的奇偶性?
3、多媒体屏幕上展示函数f (x) =x3和函数g (x) = x2的图象,并让学生分别求出x =±3,x =±2,
x =±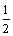 ,… 的函数值,同时令两个函数图象上对应的点在两个函数图象上闪现,让学生发现两个函数的对称性反映到函数值上具有的特性:f (–x) = – f (x),g (–x)
= g (x). 然后通过解析式给出证明,进一步说明这两个特性对定义域内的任意一个x都成立.
,… 的函数值,同时令两个函数图象上对应的点在两个函数图象上闪现,让学生发现两个函数的对称性反映到函数值上具有的特性:f (–x) = – f (x),g (–x)
= g (x). 然后通过解析式给出证明,进一步说明这两个特性对定义域内的任意一个x都成立.
2、要求学生同桌两人分别画出函数f (x) =x3与g (x) = x2的图象.
1、在初中学习的轴对称图形和中心对称图形的定义是什么?
1)两个定义:增函数、减函数;
2)两种方法:判断函数单调性的方法有:图象法、定义法.
3. 例题
例题
例1.右图是定义在闭区间[-5,5]上的函数 y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上,y=f(x)是增函数还是减函数.
解:函数y=f(x)的单调区间有[-5,-2),
[-2,1),[1,3), [3,5],
其中y=f(x)在区间[-5,-2),[1,3)上是减 函数,在区间[-2,1),[3,5]上是增函数. 这种判断函数单调性的方法称为“图象法” .
变式1:求y=x2-4 x+5的单调区间。
变式2:y=x2-a x+4在[2,4]上是单调函数,求a的取值范围。
例2.证明函数f(x)=3x+2在R上是增函数.
证明:设x1,x2是R上的任意两个实数,且x1<x2, 取值
则f(x1)-f(x2)=(3x1+2)-(3x2+2) 作差
=(3x1-3x2)+2-2=3(x1-x2). 变形
由x1<x2,得 x1-x2<0,
于是f(x1)-f(x2)<0,
即 f(x1)<f(x2) . 定号
所以,f(x)=3x+2在R上是增函数. 判断
这种判断函数单调性的方法称为“定义法” .它有五个步骤,分别是:取值、作差、变形、定号、判断.
变式1:函数f(x)=-3x+2在R上是增函数还是减函数?
变式2:函数f(x)=kx+b(k≠0)在R上是增函数还是减函数?并证明.
例3.证明函数f(x)=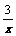 在(0, +∞)上是减函数.
在(0, +∞)上是减函数.
变式1:f(x)=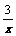 在(-∞,0)上是增函数还是减函数?
可得到f(x)=
在(-∞,0)上是增函数还是减函数?
可得到f(x)=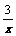 在(-∞,0)上是减函数.
在(-∞,0)上是减函数.
变式2:讨论函数f(x)=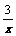 在定义域上的单调性. 结论:函数f(x)=
在定义域上的单调性. 结论:函数f(x)=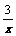 在其定义域上不具有单调性.
在其定义域上不具有单调性.
例4.证明函数f(x)=x+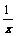 在(0,1]上是减函数.
在(0,1]上是减函数.
(思备用题,在这节课讲有一定的难度,因此,远端学校的老师根据学生的情况酌情处理.)
2.函数单调性的概念:
如果函数y=f(x)在某区间上是增函数或减函数,那么就说函数f(x)在这一区间具有(严格的)单调性,这一区间叫做y=f(x)的单调区间.
在单调区间上增函数的图象是上升的,减函数的图象是下降的.
1.增函数、减函数的概念:
一般地,设函数f(x)的定义域为I.
1)如果对于定义域I内的某个区间上的任意两个自变量的值x1,x2,当x1<x2,时,都有f(x1)<f(x2),那么就说f(x)在这个区间上是增函数.
2)如果对于定义域I内的某个区间上的任意两个自变量的值x1,x2,当x1<x2,时,都有f(x1)>f(x2),那么就说f(x)在这个区间上是减函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com