
例2.①若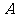 为不等式组
为不等式组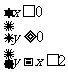 表示的平面区域,则当
表示的平面区域,则当 从-2连续变化到1时,动直线
从-2连续变化到1时,动直线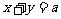 扫过
扫过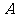 中的那部分区域的面积为 ( C )
中的那部分区域的面积为 ( C )
A.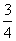 B.1 C.
B.1 C.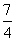 D.5
D.5
②在平面直角坐标系中,点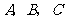 的坐标分别为
的坐标分别为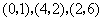 .如果
.如果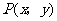 是
是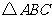 围成的区域(含边界)上的点,那么当
围成的区域(含边界)上的点,那么当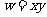 取到最大值时,点
取到最大值时,点 的坐标是 _____
的坐标是 _____ 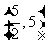
变式:
1.若实数x、y满足 则
则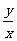 的取值范围是( D )
的取值范围是( D )
A.(0,2) B.(0,2) C.(2,+∞) D.[2,+∞)
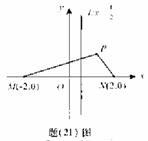
例1.如图,M(-2,0)和N(2,0)是平面上的两点,动点P满足: 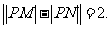
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设d为点P到直线l: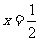 的距离,若
的距离,若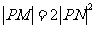 ,求
,求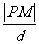 的值。
的值。
解:(I)由双曲线的定义,点P的轨迹是以M、N为焦点,实轴长2a=2的双曲线.,因此半焦距c=2,实半轴a=1,从而虚半轴b=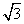 ,所以双曲线的方程为x2-
,所以双曲线的方程为x2-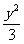 =1.
=1.
(II)由(I)及(21)图,易知|PN| 1,因|PM|=2|PN|2, ①
1,因|PM|=2|PN|2, ①
知|PM|>|PN|,故P为双曲线右支上的点,所以|PM|=|PN|+2. ②
将②代入①,得2||PN|2-|PN|-2=0,解得|PN|= ,所以|PN|=
,所以|PN|=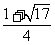 .
.
因为双曲线的离心率e=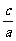 =2,直线l:x=
=2,直线l:x=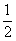 是双曲线的右准线,故
是双曲线的右准线,故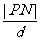 =e=2,
=e=2,
所以d=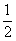 |PN|,因此
|PN|,因此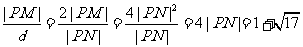
变式:
在平面直角坐标系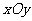 中,点P到两点
中,点P到两点 ,
,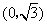 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为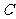 .
.
(Ⅰ)写出C的方程;
(Ⅱ)设直线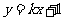 与C交于A,B两点.k为何值时
与C交于A,B两点.k为何值时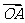
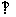
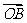 ?此时
?此时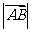 的值是多少?
的值是多少?
解:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以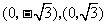 为焦点,长半轴为2的椭圆.它的短半轴
为焦点,长半轴为2的椭圆.它的短半轴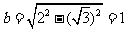 ,故曲线C的方程为
,故曲线C的方程为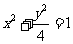 .
.
(Ⅱ)设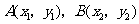 ,其坐标满足
,其坐标满足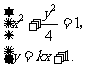
消去y并整理得 ,故
,故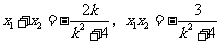 .
.
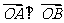 ,即
,即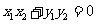 .而
.而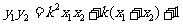 ,
,
于是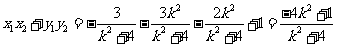 .
.
所以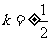 时,
时,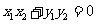 ,故
,故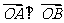 .
.
当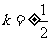 时,
时,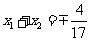 ,
,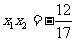 .
.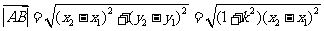 ,
,
而
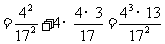 ,所以
,所以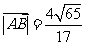 .
.
解析几何是高中数学的重点内容之一,也是高考考查的热点。高考着重考查基础知识的综合,基本方法的灵活运用,数形结合、分类整合、等价转化、函数方程思想以及分析问题解决问题的能力。其中客观题为基础题和中档题,主观题常常是综合性很强的压轴题。本专题命题的热点主要有:①直线方程;②线性规划;③直线与圆、圆锥曲线的概念和性质;④与函数、数列、不等式、向量、导数等知识的综合应用。
12.双曲线的中心为原点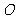 ,焦点在
,焦点在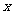 轴上,两条渐近线分别为
轴上,两条渐近线分别为 ,经过右焦点
,经过右焦点 垂直于
垂直于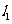 的直线分别交
的直线分别交 于
于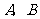 两点.已知
两点.已知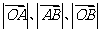 成等差数列,且
成等差数列,且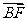 与
与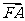 同向.
同向.
(Ⅰ)求双曲线的离心率;(Ⅱ)设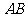 被双曲线所截得的线段的长为4,求双曲线的方程.
被双曲线所截得的线段的长为4,求双曲线的方程.
11.已知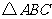 的顶点
的顶点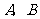 在椭圆
在椭圆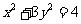 上,
上,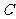 在直线
在直线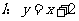 上,且
上,且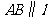 .
.
(Ⅰ)当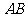 边通过坐标原点
边通过坐标原点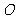 时,求
时,求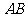 的长及
的长及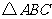 的面积;
的面积;
(Ⅱ)当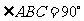 ,且斜边
,且斜边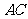 的长最大时,求
的长最大时,求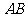 所在直线的方程.
所在直线的方程.
10.已知圆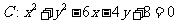 .以圆
.以圆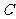 与坐标轴的交点分别作为双曲线的一个焦点和顶点,则适合上述条件的双曲线的标准方程为
与坐标轴的交点分别作为双曲线的一个焦点和顶点,则适合上述条件的双曲线的标准方程为
9.过椭圆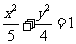 的右焦点作一条斜率为2的直线与椭圆交于
的右焦点作一条斜率为2的直线与椭圆交于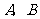 两点,
两点,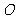 为坐标原点,则
为坐标原点,则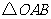 的面积为
的面积为
8.在平面直角坐标系中,椭圆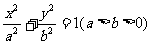 的焦距为2,以O为圆心,
的焦距为2,以O为圆心,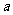 为半径的圆,过点
为半径的圆,过点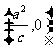 作圆的两切线互相垂直,则离心率
作圆的两切线互相垂直,则离心率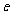 =
=
7.已知直线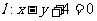 与圆
与圆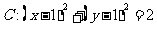 ,则
,则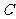 上各点到
上各点到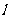 的距离的最小值为___
的距离的最小值为___
6.若双曲线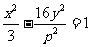 的左焦点在抛物线y2=2px的准线上,则p的值为( )
的左焦点在抛物线y2=2px的准线上,则p的值为( )
(A)2 (B)3 (C)4 (D)4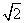
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com