
21.(本题满分12分)
解:(Ⅰ)解:以OA、OB、OS所在直线为x、y、z轴建立空间直角坐标系(如图0,则
 从而E(0,0,
从而E(0,0, ),
),
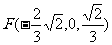 …………2分
…………2分
∴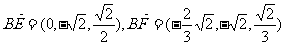
设 是平面BEF的法向量,
是平面BEF的法向量,
∴
令x=-1,则n=(-1,2,4) ………………5分
又 是底面ABCD的法向量,
是底面ABCD的法向量,
∴
故平面BEF与底面ABCD所成二面角的余弦值为 ………………7分
………………7分
(Ⅱ)证明:由(Ⅰ)知

当 是单调递增函数;
是单调递增函数;
∵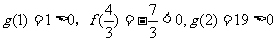
∴方程 内分别有唯一实数根
…………12分
内分别有唯一实数根
…………12分
∴存在正整数m=1使得方程 在区间(1,2)上有且只有两个不相等的实数根. ………………14分
在区间(1,2)上有且只有两个不相等的实数根. ………………14分
20.(本题满分12分)
解:(Ⅰ)甲获胜分为两种情况,即甲以2:0获胜或以2:1获胜,
这两种情况是互斥的. ………………2分
甲以2:0获胜的概率为P1=0.62=0.36;
甲以2:1获胜的概率为P2= ·0.6·0.4·0.6=0.288.
·0.6·0.4·0.6=0.288.
故甲获胜的概率为P=P1+P2=0.36+0.288=0.648 …………6分
(Ⅱ)ζ的取值为2,3 ………………7分
P(ζ=2)=0.62+0.42=0.36+0.16=0.52. …………7分
P(ζ=3)= ·0.62·0.4+
·0.62·0.4+ ·0.42·0.6=0.288+0.192=0.48.
·0.42·0.6=0.288+0.192=0.48.
∴ζ的分布列为  ………………10分
………………10分
∴E(ζ)=2×0.52+3×0.48=2.48 ……………………12分
22.已知向量i=(1,0),j=(0,1),规定 ,其中
,其中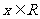 ,
,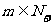 ,且
,且 处取得极值,在x=2处的切线的方向向量为
处取得极值,在x=2处的切线的方向向量为
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)是否存在正整数m,使得方程 内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.
内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.

由 …………………………8分
…………………………8分
解得  ……………………12分
……………………12分

21.(本小题满分12分)
 如图,在棱长都为2的正四棱锥S-ABCD中,O是底面中心,E是SO的中点,F在棱SC上且
如图,在棱长都为2的正四棱锥S-ABCD中,O是底面中心,E是SO的中点,F在棱SC上且 ,P是棱SA上的点.
,P是棱SA上的点.
(Ⅰ)求平面BEF与底面ABCD所成角的余弦值;
(Ⅱ)试证DP不可能与BF垂直.
20.(本小题满分12分)
甲、乙两队进行一场排球比赛,根据以往比赛的胜负情况知道,每一局比赛甲胜的概率为0.6,已胜的概率为0.4. 本场比赛采用三局两胜制.
(Ⅰ)求甲获胜的概率;
(Ⅱ)设ζ为本场比赛的局数,求ζ的概率分布和数学期望.
19.(本小题满分12分)
已知函数 ,且任意的n1,n2
,且任意的n1,n2  ,有
,有
(Ⅰ)求 的值;
的值;
(Ⅱ)试猜想 的解析式,并给出证明.
的解析式,并给出证明.
18.(本小题满分12分)
已知p>0且二项式 的展开式中,第8项的系数和第10项的系数都小于常数项,求p的取值范围.
的展开式中,第8项的系数和第10项的系数都小于常数项,求p的取值范围.
17.(本小题满分12分)
已知虚数z满足
(Ⅰ)求|z|的值;
(Ⅱ)若 ,求实数m的值.
,求实数m的值.
16.用一条直线截正方形的一个角,得到边长为a,b,c的直角三角形(图1);用一个平面截正方体的一个角,得到以截面为底面且面积为S,三个侧面面积分别为S1,S2,S3的三棱锥(图2). 试类比图1的结论,写出图2的结论.

15.如图,在棱长为2的正方体中,E是棱AA1的中点,则棱BB1与平面BED1所成角的正弦值等于 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com