
3、下列各图中,可表示函数y=f(x)的图象的只可能是( )
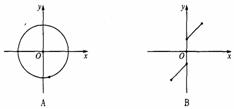

2、设全集 ={1,2,3,4,5},
={1,2,3,4,5},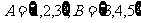 ,则集合
,则集合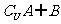 的子集个数为( )
的子集个数为( )
(A) 3 (B) 4 (C) 7 (D) 8
1、已知集合A= ,B=
,B=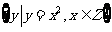 ,则A与B的关系是( )
,则A与B的关系是( )
(A) A (B)
(B)  (C)
(C)  (D)
(D) 
21.(本小题满分13分)
对于定义域为D的函数 ,若同时满足下列条件:①
,若同时满足下列条件:①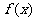 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[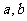 ]
]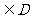 ,使
,使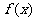 在[
在[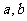 ]上的值域为[
]上的值域为[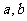 ];那么把
];那么把 (
(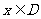 )叫闭函数。
)叫闭函数。
(1)求闭函数 符合条件②的区间[
符合条件②的区间[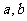 ];
];
(2)判断函数 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)判断函数 是否为闭函数?若是闭函数,求实数
是否为闭函数?若是闭函数,求实数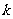 的取值范围。
的取值范围。
20.(本小题满分13分)已知函数 。
。
(Ⅰ)当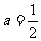 时,利用函数单调性的定义判断并证明
时,利用函数单调性的定义判断并证明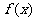 的单调性,并求其值域;
的单调性,并求其值域;
(Ⅱ)若对任意 ,求实数a的取值范围。
,求实数a的取值范围。
19. (本小题满分13分)函数 ,
,
(1)若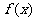 的定义域为[-2,1],求实数a的值.
的定义域为[-2,1],求实数a的值.
(2)若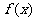 的定义域为
的定义域为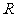 ,求实数
,求实数 的取值范围.
的取值范围.
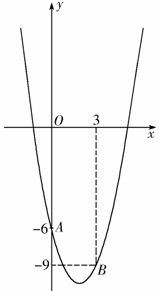
18.(本题12分)如图,已知抛物线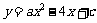 经过点
经过点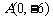 和
和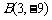 ,
,
(1)求出抛物线的解析式;
(2)写出抛物线的对称轴方程及顶点坐标;
 (3)点P(m,m)
(3)点P(m,m)  与点Q均在抛物线上(其中m>0),且这两点关于抛物线的对称轴 对称,求m的值及点Q的坐标;
与点Q均在抛物线上(其中m>0),且这两点关于抛物线的对称轴 对称,求m的值及点Q的坐标;
(4)在满足(3 )的情况下,在抛物线的对称轴上
)的情况下,在抛物线的对称轴上
寻找一点M,使得△QMA的周长最小.
17、(本小题满分12分)
某公司要将一批不易存放的蔬菜从A地运到B 地,有汽车、火车两种运输工具可供选择,两种运输工具的主要参考数据如下表:
|
运输工具 |
途中速度 (km/h) |
途中费用 (元/km) |
装卸时间 (h) |
装卸费用 (元) |
|
汽车 |
50 |
8 |
2 |
1000 |
|
火车 |
100 |
4 |
4 |
2000 |
若这批蔬菜在运输过程(含装卸时间)中损耗为300元/h,设A、B 两地距离为 km
km
(I)设采用汽车与火车运输的总费用分别为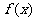 与
与 ,求
,求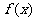 与
与 ;
;
(II)试根据A、B两地距离大小比较采用哪种运输工具比较好(即运输总费用最小).
(注:总费用=途中费用+装卸费用+损耗费用)
16.(本小题满分12分)
已知集合 ,
,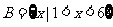 ,
,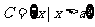 ,
,  R.
R.
⑴ 求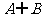 ,(CuA)∩B;
,(CuA)∩B;
⑵ 如果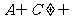 ,求a的取值范围.
,求a的取值范围.
15.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com