
3.将锐角为60°,边长为a的菱形ABCD沿较短的对角线折成60°的二面角,则AC与BD的距离为
A.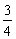 a B.
a B.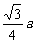 C.
C.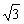 a
D.
a
D.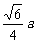
2.α-a-β的平面角是锐角θ,α内一点A到棱a的距离为4,点A到面β的距离为3,则tanθ的值等于
A.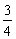 B.
B.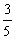 C.
C.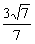 D.
D.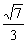
1.已知点A、B、C、D的坐标分别为(-1,0,1),(0,0,1),(2,2,2)(0,0,3),则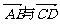 所成的角为
所成的角为
A.arccos(-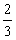 ) B.-arccos(-
) B.-arccos(-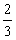 )
)
C.arccos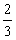 D.-arccos
D.-arccos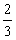
8.在棱长为a的正四面体ABCD中,M、E分别是棱BD、BC的中点,N是BE的中点,连结DE、MN,求直线DE与平面AMN间的距离.
基础训练34(B) 夹角与距离的计算
●训练指要
掌握空间有关角和距离的确定方法、范围,熟练地计算空间的角和距离.
7.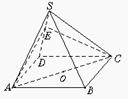 如图,正四棱锥S-ABCD的所有棱长都相等,过底面对角线 AC作平行于侧棱SB的截面交SD于E.
如图,正四棱锥S-ABCD的所有棱长都相等,过底面对角线 AC作平行于侧棱SB的截面交SD于E.
(1)求AB与SC所成角的大小;
(2)求二面角E-AC-D的大小;
(3)求直线BC与平面EAC所成角的大小.
6.如图,在正三棱锥P-ABC中,侧棱长3 cm,底面边长2 cm,E是BC的中点,EF⊥PA,垂足为F.
(1)求证:EF为异面直线PA与BC的公垂线段;
(2)求异面直线PA与BC间的距离.
5.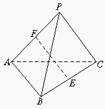 三个两两垂直的平面,它们的三条交线交于一点O,点P到三个平面的距离的比为1∶2∶3,PO=2
三个两两垂直的平面,它们的三条交线交于一点O,点P到三个平面的距离的比为1∶2∶3,PO=2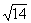 ,则P点到这三个平面的距离分别是_________.
,则P点到这三个平面的距离分别是_________.
4.二面角α-l-β的面α内有一条直线a与l成45°的角,若这个二面角的平面角也是45°,则直线a与平面β成角的度数为_________.
2.给出下列四个命题:
①如果直线a∥平面α,a 平面β,且α∥β,则a与平面α的距离等于平面α与β的距离;
平面β,且α∥β,则a与平面α的距离等于平面α与β的距离;
②两条平行直线分别在两个平行平面内,则这两条平行直线的距离等于这两个平面间的距离;
③异面直线a、b分别在两个平行平面内,则a、b的距离等于这两个平面的距离;
④若点A在平面α内,平面α和β平行,则A到平面β的距离等于平面α与平面β的距离.
其中正确的命题的个数是
A.1 B.2 C.3 D.4
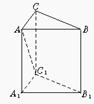 3.如图,正三棱柱ABC-A1B1C1的各条棱长均相等,则AC1与平面BB1C1C所成角的余弦值等于
3.如图,正三棱柱ABC-A1B1C1的各条棱长均相等,则AC1与平面BB1C1C所成角的余弦值等于
A.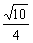 B.
B.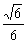
C.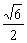 D.
D.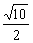
1.(2001年全国高考题)一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜,记三种盖法屋顶面积分别为P1、P2、P3.

若屋顶斜面与水平面所成的角都是α,则
A.P3>P2>P1 B.P3>P2=P1
C.P3=P2>P1 D.P3=P2=P1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com