3．下图表示新鲜菠菜叶中四种色素的相对含量及在滤纸条上的分离情况。下列说法不正确的是

A．叶绿体中的四种色素分布在类囊体薄膜上

B．四种色素均可溶于有机溶剂无水乙醇中

C．四种色素在层析液中溶解度最大的是甲

D．发黄菠菜叶中色素含量显著减少的是甲和乙

2．细胞膜上的蛋白质分子

A．在细胞膜内外侧对称分布　　　　　 B．是不能运动的

C．与细胞膜的功能有关　　　　　　　 D．在细胞膜内侧与糖类结合形成糖蛋白

1．下列物质或细胞结构中，没有核糖参与组成的是

A．转运RNA　　　 B．质粒　　　　　 C．核糖体　　　　　 D．ATP

23．设数列{a_n}满足a₁＝a，a_n+1＝a_n²+a₁，．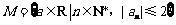

(1)当a∈(－∞，－2)时，求证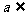：M；

(2)当a∈(0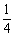，］时，求证：a∈M；

(3)当a∈(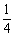，+∞)时，判断元素a与集合M的关系，并证明你的结论．

南通市2010届高三第二次调研测试

22．一个暗箱中有形状和大小完全相同的3只白球与2只黑球，每次从中取出一只球，取到白球得2分，取到黑球得3分．甲从暗箱中有放回地依次取出3只球．

(1)写出甲总得分ξ的分布列；

(2)求甲总得分ξ的期望E(ξ)．

21．[选做题]在A，B，C，D四小题中只能选做2题，每小题10分，共计20分．请在答题卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．

A．选修4－1　几何证明选讲

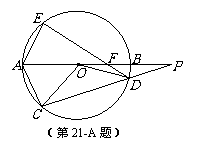如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC， DE交AB于点F．求证：△PDF∽△POC．

B．选修4－2　矩阵与变换

若点A(2，2)在矩阵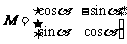对应变换的作用下得到的点为B(－2，2)，求矩阵M的逆矩阵．

C．选修4－4　坐标系与参数方程

已知极坐标系的极点O与直角坐标系的原点重合，极轴与x轴的正半轴重合，曲线C₁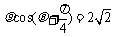：与曲线C₂：(t∈R)交于A、B两点．求证：OA⊥OB．

D．选修4－5　不等式选讲

已知x，y，z均为正数．求证：．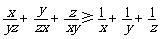

[必做题]第22题、第23题，每小题10分，共计20分．请在答题卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．

20．(本小题满分16分)

设函数f(x)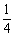＝x⁴+bx²+cx+d，当x＝t₁时，f(x)有极小值．

(1)若b＝－6时，函数f(x)有极大值，求实数c的取值范围；

(2)在(1)的条件下，若存在实数c，使函数f(x)在闭区间［m－2，m+2］上单调递增，求实数m的取值范围；

(3)若函数f(x)只有一个极值点，且存在t₂∈(t₁，t₁+1)，使f ′(t₂)＝0，证明：函数g(x)＝f(x)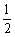－x²+t₁x在区间(t₁，t₂)内最多有一个零点．

附加题部分

19．(本小题满分16分)

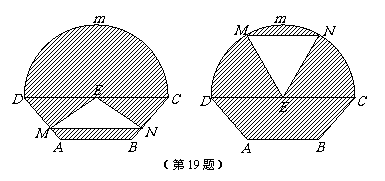
某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD是等腰梯形，其中高0.5米，AB=1米， CD=2a(a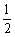＞)米．上部CmD是个半圆，固定点E为CD的中点．△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风)，MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆．

(1)设MN与AB之间的距离为x米，试将三角通风窗EMN的通风面积S(平方米)表示成关于x的函数；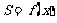

(2)当MN与AB之间的距离为多少米时，三角通风窗EMN的通风面积最大？并求出这个最大面积．

18．(本小题满分15分)

平面直角坐标系xOy中，已知⊙M经过点F₁(0，－c)，F₂(0，c)，A(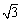c，0)三点，其中c＞0．

(1)求⊙M的标准方程(用含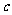的式子表示)；

(2)已知椭圆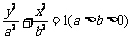(其中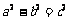)的左、右顶点分别为D、B，

⊙M与x轴的两个交点分别为A、C，且A点在B点右侧，C点在D点右侧．

①求椭圆离心率的取值范围；

②若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上，问直线MF₁与直线DF₂的交点是否在一条定直线上？若是，请求出这条定直线的方程；若不是，请说明理由．

17．(本小题满分15分)

设等比数列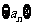的首项为a₁，公比为q，且q>0，q≠1.

(1)若a₁=q^m，m∈Z，且m≥－1，求证：数列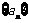中任意不同的两项之积仍为数列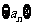

中的项；

(2)若数列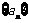中任意不同的两项之积仍为数列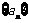中的项，求证：存在整数m，且

m≥－1，使得a₁=q^m.