
1.设集合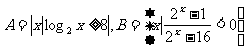 则
则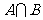 = ( )
= ( )
A.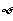 B.
B.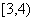 C.
C.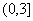 D.
D.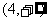
2.(2010·创新题)某医疗研究所为了检验某种血清预防感冒的作用,把500名使用血清的人与另外500名未用血清的人一年中的感冒记录作比较,提出假设H0:“这种血清不能起到预防感冒的作用”,利用2×2列联表计算得K2≈3.918,经查对临界值表知P(K2≥3.841)≈0.05.
p:有95%的把握认为“这种血清能起到预防感冒的作用”;
q:若某人未使用该血清,那么他在一年中有95%的可能性得感冒;
r:这种血清预防感冒的有效率为95%;
s:这种血清预防感冒的有效率为5%.
则下列结论中,正确结论的序号是________.(把你认为正确的命题序号都填上)
①p∧綈q;②綈p∧q;③(綈p∧綈q)∧(r∨s);④(p∨綈r)∧(綈q∨s).
解析:由题意,得K2≈3.918,P(K2≥3.841)≈0.05,所以只有p正确,即有95%的把握认为“这种血清能起到预防感冒的作用”,由真值表知①、④为真命题.
答案:①④
1.(★★★★)①合情推理是由特殊到一般的推理,得到的结论不一定正确,演绎推理是由一般到特殊的推理,得到的结论一定正确;
②一般地,当r的绝对值大于0.75时,认为两个变量之间有很强的线性相关关系,如果变量y与x之间的相关系数r=-0.956 8,则变量y与x之间具有线性关系;
③用独立性检验(2×2列联表法)来考察两个分类变量是否有关系时,算出的随机变量K2的值越大,说明“x与y有关系”成立的可能性越大;
④命题p:∃x∈R使得x2+x+1<0,则綈p:∀x∈R均有x2+x+1≥0.
其中结论正确的序号为________.(写出你认为正确的所有结论的序号)
解析:②通过统计假设,查表得结论正确;③参考两个分类变量x和y有关系的可信度表:k2的值越大,说明“x与y有关系”成立的可能性越大;④正确,命题p:∃x∈R使得p(x),则綈p:∀x∈R均有綈p(x).
答案:②③④
10.某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
|
x |
2 |
4 |
5 |
6 |
8 |
|
y |
30 |
40 |
60 |
50 |
70 |
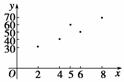
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?
解答:(1)根据表中所列数据可得散点图如下:
(2)列出下表,并用科学计算器进行有关计算.
|
i |
1 |
2 |
3 |
4 |
5 |
|
xi |
2 |
4 |
5 |
6 |
8 |
|
yi |
30 |
40 |
60 |
50 |
70 |
|
xiyi |
60 |
160 |
300 |
300 |
560 |
因此,x==5,y==50,=145,=13 500,iyi=1 380.
于是可得b===6.5;
a=y-bx=50-6.5×5=17.5,因此,所求回归直线方程是=6.5x+17.5.
(3)据上面求得的回归直线方程,当广告费支出为10百万元时,
=6.5×10+17.5=82.5(百万元),
即这种产品的销售收入大约为82.5百万元.

9.(2010·江苏徐州调研)在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520名女性中有6人患色盲.
(1)根据以上数据建立一个2×2列联表;
(2)若认为“性别与患色盲有关系”,则出错的概率会是多少?
附临界值参考表:
|
P(K2≥x0) |
0.10 |
0.05 |
0.025 |
0.10 |
0.005 |
0.001 |
|
x0 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
解答:(1)
|
|
患色盲 |
不患色盲 |
总计 |
|
男 |
38 |
442 |
480 |
|
女 |
6 |
514 |
520 |
|
总计 |
44 |
956 |
1
000 |
(2)假设H0:“性别与患色盲没有关系”,根据(1)中2×2列联表中数据,可求得
K2=≈27.14,
又P(K2≥10.828)=0.001,即H0成立的概率不超过0.001,
故若认为“性别与患色盲有关系”,则出错的概率为0.001.
8.(2009·安徽蚌埠)已知x、y之间的一组数据如下表:
|
x |
1 |
3 |
6 |
7 |
8 |
|
y |
1 |
2 |
3 |
4 |
5 |
对于表中数据,甲、乙两同学给出的拟合直线分别为y=x+1与y=x+,试利用最小二乘法判断哪条直线拟合程度更好?
解答:用y=x+1作为拟合直线时,所得y值与y的实际值的差的平方和为
s1=2+(2-2)2+(3-3)2+2+2=;
用y=x+作为拟合直线时,所得y值与y的实际值的差的平方和为
s2=(1-1)2+(2-2)2+2+(4-4)2+2=.
∵s2<s1,故用直线y=x+拟合程度更好.
7.(2010·山东潍坊调研)给出下列四个命题:
 ①∀x∈R,cos
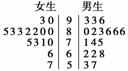
x=sin+sin一定不成立;②今年初某医疗研究所为了检验“达菲(药物)”对甲型H1N1流感病毒是否有抑制作用,把墨西哥的患者数据库中的500名使用达菲的人与另外500名未用达菲的人一段时间内患甲型H1N1流感的疗效记录作比较,提出假设H0:“达菲不能起到抑制甲型H1N1流感病毒的作用”,利用2×2列联表计算得K2≈3.918,经查对临界值表知P(K2≥3.841)≈0.05,说明达菲抑制甲型H1N1流感病毒的有效率为95%;③|a·b|=|a||b|是|λa+μb|=|λ||a|+|μ||b|成立的充要条件;④如右图的茎叶图是某班在一次测验时的成绩:可断定:女生成绩比较集中,整体水平稍高于男生.
①∀x∈R,cos
x=sin+sin一定不成立;②今年初某医疗研究所为了检验“达菲(药物)”对甲型H1N1流感病毒是否有抑制作用,把墨西哥的患者数据库中的500名使用达菲的人与另外500名未用达菲的人一段时间内患甲型H1N1流感的疗效记录作比较,提出假设H0:“达菲不能起到抑制甲型H1N1流感病毒的作用”,利用2×2列联表计算得K2≈3.918,经查对临界值表知P(K2≥3.841)≈0.05,说明达菲抑制甲型H1N1流感病毒的有效率为95%;③|a·b|=|a||b|是|λa+μb|=|λ||a|+|μ||b|成立的充要条件;④如右图的茎叶图是某班在一次测验时的成绩:可断定:女生成绩比较集中,整体水平稍高于男生.
其中真命题的序号是________.(填上所有真命题的序号)
解析:对于①,等式展开后可化简为asin x+bcos x=0的形式,可知一定有解;对于②,正确解释是:有95%的把握认为“达菲对甲型H1N1流感病毒有抑制作用”;对于③,由向量模的性质知不正确.
答案:④
6.已知回归直线方程=0.5x-0.801,则当x=25时,y的估计值是________.
解析:将x=25代入=0.5x-0.801可得.
答案:11.699
5.(2009·江苏徐州)独立性检验中的统计假设就是假设两个研究对象Ⅰ和Ⅱ________.
答案:相互独立(没有关系)
4.(2009·江苏徐州)在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )
①若K2的观测值满足K2≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;②从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病;③从统计量中得知有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误.
A.① B.①③ C.③ D.②
解析:①推断在100个吸烟的人中必有99人患有肺病,说法错误,排除A,B,③正确.
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com