
19.(本小题满分14分)
(本小题主要考查函数与导数等知识,考查分类讨论,化归与转化的数学思想方法,以及推理论证能力和运算求解能力)
(1)解:∵ ,∴
,∴ .
.
令 ,得
,得 .
.
①若 ,则
,则 ,
,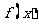 在区间
在区间 上单调递增,此时函数
上单调递增,此时函数 无最小值.
无最小值.
②若 ,当
,当 时,
时, ,函数
,函数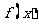 在区间
在区间 上单调递减,
上单调递减,
当 时,
时, ,函数
,函数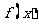 在区间
在区间 上单调递增,
上单调递增,
所以当 时,函数
时,函数 取得最小值
取得最小值 .
.
③若 ,则
,则 ,函数
,函数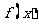 在区间
在区间 上单调递减,
上单调递减,
所以当 时,函数
时,函数 取得最小值
取得最小值 .
.
综上可知,当 时,函数
时,函数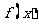 在区间
在区间 上无最小值;
上无最小值;
当 时,函数
时,函数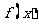 在区间
在区间 上的最小值为
上的最小值为 ;
;
当 时,函数
时,函数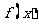 在区间
在区间 上的最小值为
上的最小值为 .
.
(2)解:∵ ,
, ,
,
∴ 
 .
.
由(1)可知,当 时,
时, .
.
此时 在区间
在区间 上的最小值为
上的最小值为 ,即
,即 .
.
当 ,
, ,
, ,
,
∴ .
.
曲线 在点
在点 处的切线与
处的切线与 轴垂直等价于方程
轴垂直等价于方程 有实数解.
有实数解.
而 ,即方程
,即方程 无实数解.
无实数解.
故不存在 ,使曲线
,使曲线 在点
在点 处的切线与
处的切线与 轴垂直.
轴垂直.
18.(本小题满分14分)
(本小题主要考查空间线面关系、空间向量及坐标运算等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力)
(1)证明:∵ 垂直于圆
垂直于圆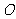 所在平面,
所在平面, 在圆
在圆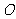 所在平面上,
所在平面上,
∴
 .
.
在正方形 中,
中, ,
,
∵ ,∴
,∴ 平面
平面 .
.
∵ 平面
平面 ,
,
∴平面 平面
平面 .
.
(2)解法1:∵ 平面
平面 ,
, 平面
平面 ,
,
∴ .
.
 ∴
∴ 为圆
为圆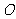 的直径,即
的直径,即 .
.
设正方形 的边长为
的边长为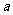 ,
,
在 △
△ 中,
中, ,
,
在 △
△ 中,
中, ,
,
由 ,解得,
,解得, .
.
∴ .
.
过点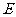 作
作 于点
于点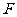 ,作
,作 交
交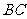 于点
于点 ,连结
,连结 ,
,
由于 平面
平面 ,
, 平面
平面 ,
,
∴ .
.
∵ ,
,
∴ 平面
平面 .
.
∵ 平面
平面 ,
,
∴ .
.
∵ ,
, ,
,
∴ 平面
平面 .
.
∵ 平面
平面 ,
,
∴ .
.
∴ 是二面角
是二面角 的平面角.
的平面角.
在 △
△ 中,
中, ,
, ,
, ,
,
∵ ,
,
∴ .
.
在 △
△ 中,
中, ,
,
∴ .
.
故二面角 的平面角的正切值为
的平面角的正切值为 .
.
解法2:∵ 平面
平面 ,
, 平面
平面 ,
,
∴ .
.
∴ 为圆
为圆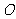 的直径,即
的直径,即 .
.
设正方形 的边长为
的边长为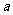 ,
,
在 △
△ 中,
中, ,
,
在 △
△ 中,
中, ,
,
由 ,解得,
,解得, .
.
∴ .
.
 以
以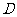 为坐标原点,分别以
为坐标原点,分别以 、
、 所在的直线为
所在的直线为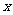 轴、
轴、 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则 ,
, ,
, ,
, ,.com
,.com
 .
.
设平面 的法向量为
的法向量为 ,
,
则 即
即
取 ,则
,则 是平面
是平面 的一个法向量.
的一个法向量.
设平面 的法向量为
的法向量为 ,
,
则 即
即
取 ,则
,则 是平面
是平面 的一个法向量.
的一个法向量.
∵ ,
,
∴ .
.
∴ .
.
故二面角 的平面角的正切值为
的平面角的正切值为 .
.
17.(本小题满分12分)
(本小题主要考查随机变量的分布列、数学期望等知识,考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识)
解:设 表示摸球后所得的奖金数,由于参与者摸取的球上标有数字1000,800,600,0,当摸到球上标有数字0时,可以再摸一次,但奖金数减半,即分别为500,400,300,0.
表示摸球后所得的奖金数,由于参与者摸取的球上标有数字1000,800,600,0,当摸到球上标有数字0时,可以再摸一次,但奖金数减半,即分别为500,400,300,0.
则 的所有可能取值为1000,800,600,500,400,300,0.
的所有可能取值为1000,800,600,500,400,300,0.
依题意得
 ,
,
 ,
,
则 的分布列为
的分布列为
奖金 |
1000 |
800 |
600 |
500 |
400 |
300 |
0 |
概率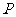 |
 |
 |
 |
 |
 |
 |
 |
所以所求期望值为

 元.
元.
答:一个参与抽奖活动的人可得奖金的期望值是675元.
16.(本小题满分12分)
(本小题主要考查三角函数性质和三角函数的基本关系等知识,考查化归与转化的数学思想方法,以及运算求解能力)
(1)解:∵ ,
,
∴函数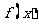 的最小正周期为
的最小正周期为 .
.
(2)解:∵函数 ,
,
又 的图像的对称轴为
的图像的对称轴为 (
( ),
),
令 ,
,
将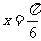 代入,得
代入,得 (
( ).
).
∵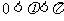 ,∴
,∴ .
.
14. 15.3
15.3
9.7 10.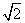 11.
11. 12.
12. 13.①②③
13.①②③
21.(本小题满分14分)
设数列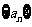 的前
的前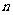 项和为
项和为 ,且对任意的
,且对任意的 ,都有
,都有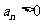 ,
, .
.
(1)求 ,
, 的值;
的值;
(2)求数列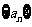 的通项公式
的通项公式 ;
;
(3)证明: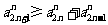 .
.
广州市东风中学2010-2011年度高三综合训练(4)
理科数学
20.(本小题满分14分)
已知点 ,直线
,直线 :
: ,
,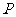 为平面上的动点,过点
为平面上的动点,过点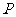 作直线
作直线 的垂线,垂足为
的垂线,垂足为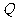 ,且
,且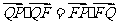 .
.
(1)求动点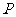 的轨迹
的轨迹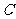 的方程;
的方程;
(2)已知圆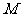 过定点
过定点 ,圆心
,圆心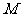 在轨迹
在轨迹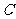 上运动,且圆
上运动,且圆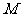 与
与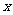 轴交于
轴交于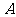 、
、 两点,设
两点,设 ,
, ,求
,求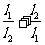 的最大值.
的最大值.
19.(本小题满分14分)
已知 ,函数
,函数 ,
, (其中
(其中 为自然对数的底数).
为自然对数的底数).
(1)求函数 在区间
在区间 上的最小值;
上的最小值;
(2)是否存在实数 ,使曲线
,使曲线 在点
在点 处的切线与
处的切线与 轴垂直? 若存在,求出
轴垂直? 若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
18.(本小题满分14分)
如图6,正方形 所在平面与圆
所在平面与圆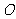 所在平面相交于
所在平面相交于 ,线段
,线段 为圆
为圆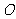 的弦,
的弦, 垂直于圆
垂直于圆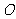 所在平面,垂足
所在平面,垂足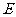 是圆
是圆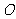 上异于
上异于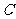 、
、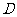 的点,
的点, ,圆
,圆 的直径为9.
的直径为9.
(1)求证:平面 平面
平面 ;
;
(2)求二面角 的平面角的正切值.
的平面角的正切值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com