4、函数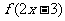的图象，可由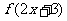的图象经过下述变换得到(　 )

　　A．向左平移6个单位　　 　B．向右平移6个单位

　　C．向左平移3个单位　　 　D．向右平移3个单位

3、设函数y=f(x)的定义域为R，则函数y=f(x-1)与y=f(1-x)的图象关系为　　　　　 ( 　　)

A、直线y=0对称　　 B、直线x=0对称

C、直线y=1对称　　　 D、直线x=1对称

2、(2006广东7)　 函数y=f(x)的反函数y=f ^-1(x)的图象与y轴交于点P(0,2)(如图所示)，则方程f(x)=0的根是x=　　 (　 )

A. 4　　 B. 3　　 C. 2　　 D. 1

1、若把函数y=f(x)的图像作平移，可以使图像上的点P(1，0)变换成点Q(2，2)，则函数y=f (x)的图像经此变换后所得图像对应的函数为 (　 )

A.y=f(x-1)+2　　　　　 B.y=f(x-1)-2

C.y=f(x+1)+2　 　　　　D.y=f(x+1)-2

8、函数y=f(a+x)与 y=f(x-b)的图象关于直线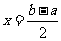对称。

证明：略

特例：函数y=f(a+x)与 y=f(a-x)的图象关于直线x=0对称。

7、若f(x)满足f(a+x)+f(b-x)=c则f(x)的图象关于点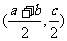中心对称。

证明：设P(x,y)是图象上任一点，则y=f(x)；

由中点公式得 P关于点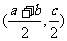对称的点为Q(a+b-x,c-y).

设t=b-x即x=b-t代入f(a+x)+f(b-x)=c得

f(t)=c-f(a+b-t)即f(a+b-x) =c- f(x)=c-y,即Q在图象上。

所以f(x)的图象象关于点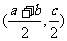中心对称。

特例：若f(a+x)+f(a－x)=2c则f(x)的图象以点(a,c)为对称中心.

6、若f(x)满足f(a+x)=-f(b－x)则f(x)的图象以为对称中心;特例：若f(a+x)=-f(a－x)则f(x)的图象以点(a,0)为对称中心。

5、若f(x)满足f(a+x)=f(b－x)则f(x)的图象以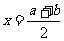为对称轴;特例：若f(a+x)=f(a－x)则f(x)的图象关于x=a对称。

4、奇偶函数图象的对称性，互为反函数的图象的对称关系；

3、要理解图象变换与函数式的变换之间的关系，常见的

图象变换有：平移、伸缩、对称、旋转等

(1)平移变换

函数y=f(x+a)(a≠0)的图象--把函数y=f(x)的图象向左(a＞0)或向右(a＜0)平移|a|；

函数y=f(x)+b(b≠0)的图象--把函数y=f(x)的图象向上(b＞0)或向下(b＜0)平移|b|

函数y=f(x+a)+b(b≠0)的图象呢？

函数y=f(x)的图象按向量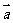=(h,k)平移后得函数y=f(x-h)+k

　(2)伸缩变换

函数y=Af(x)(A＞0，A≠1)的图象--把函数y=f(x)的图象上各点的纵坐标伸长(A＞1)或缩短(0＜A＜1)成原来的A倍；

函数y=f(ωx)(ω＞0，ω≠1)的图象--把函数y=f(x)的图象上各点的横坐标伸长(0<ω<1)或缩短(ω>1)为原来的1/ω；

说出y=Asin(ωx+φ)与y=sinx之间的关系--

(3)对称变换

函数y=f(-x)的图象与y=f(x)的图象关于y轴对称(即把(x,y)换成(-x,y))；

函数y=-f(x)的图象与y=f(x)的图象关于x轴对称；(即把(x,y)换成(x,-y))

函数y=-f(-x)的图象与y=f(x)的图象关于原点对称(即把(x,y)换成(-x,-y))；

函数y=f ^-1(x)的图象与y=f(x)的图象关于直线y=x对称；

函数y=f(|x|)的图象--把y=f(x)在y轴右方的图象换成y轴左边的对称图形即可；

函数y=|f(x)|的图象--把y=f(x)的图象在x轴下方的翻折到x轴上方而得到．