
17.解:甲选手胜乙选手的局数作为随机变量ξ,它的取值共有0、1、2、3四个值.
1)当ξ=0时,本场比赛共三局,甲选手连负三局,
P(ξ=0)=(1-0.6)3=0.064;
2)当ξ=1时,本场比赛共四局,甲选手负第四局,且前三局中,甲胜一局,
P(ξ=1)=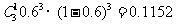 ;
;
3)当ξ=2时,本场比赛共五局,甲选手负第五局,且前四局中,甲胜二局,
P(ξ=2)= ;
;
4)当ξ=3时,本场比赛共三局、或四局、或五局.其中共赛三局时,甲连胜这三局;共赛四局时,第四局甲胜,且前三局中甲胜两局;共赛五局时,第五局甲胜,且前四局中甲胜两局;
P(ξ=3)=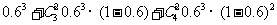 =0.68256
=0.68256
ξ的概率分布列为:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
0.064 |
0.1152 |
0.13824 |
0.68256 |
Eξ=0´P(ξ=0)+ 1´ P(ξ=1)+2´ P(ξ=2)+3´ P(ξ=3)
=0´0.064+1´0.1152+2´0.13824+3´0.68256=2.43926»2.4394.
16.解:(1)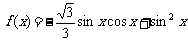
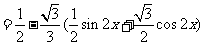
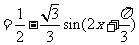
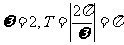 .当
.当 时,
时,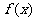 取最大值
取最大值 .
.
(2)当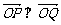 时,
时,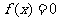 ,即
,即 ,
,
解得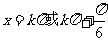 ,
,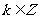 .
.
15.解:1)当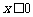 时,即解
时,即解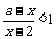 ,
,
即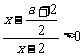 ,不等式恒成立,即
,不等式恒成立,即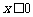 ;
;
2)当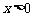 时,即解
时,即解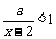 ,即
,即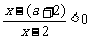 ,因为
,因为 ,所以
,所以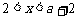 .
.
由1)、2)得,原不等式解集为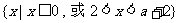 .
.
13. 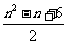 ; 14. 6.42
; 14. 6.42
9. i; 10.  11.10; 12.(2,1);
11.10; 12.(2,1);
DACB BCDA
20.(本小题满分14分)
已知A、B、C是直线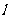 上的不同的三点,O是直线外一点,向量
上的不同的三点,O是直线外一点,向量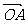 、
、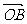 、
、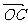 满足
满足 ,记
,记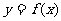 .
.
(1)求函数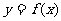 的解析式;(2)若
的解析式;(2)若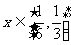 ,
,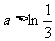 ,证明:不等式
,证明:不等式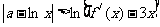 成立;(3)若关于
成立;(3)若关于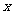 的方程
的方程 在
在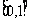 上恰有两个不同的实根,求实数
上恰有两个不同的实根,求实数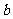 的取值范围.
的取值范围.
广州市东风中学2010-2011年度高三综合训练(5)
理科数学
19. (本小题满分14分) 已知数列
(本小题满分14分) 已知数列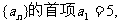 前n项和为Sn,
前n项和为Sn,
且Sn+1=2Sn+n+5(n∈N*).
(Ⅰ)证明数列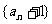 是等比数列;
是等比数列;
(Ⅱ)令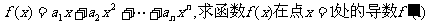 .
.
18.(本小题满分14分) 如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是底面边长的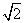 倍,P为侧棱SD上的点.(Ⅰ)求证:AC⊥SD; (Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小;
倍,P为侧棱SD上的点.(Ⅰ)求证:AC⊥SD; (Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小;
17.(本小题满分14分)一次国际乒乓球比赛中,甲、乙两位选手在决赛中相遇,根据以往经验,单局比赛甲选手胜乙选手的概率为0.6,本场比赛采用五局三胜制,即先胜三局的选手获胜,比赛结束.设全局比赛相互间没有影响,令ξ为本场比赛甲选手胜乙选手的局数(不计甲负乙的局数),求ξ的概率分布和数学期望(精确到0.0001).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com