
2.下列各句中,标点符号使用正确的一句是 ( )
A.中国跳水队领队在出征雅典世界杯赛前表示,“这次奥运会前的热身赛预定完成三项任务,感受场馆,观察对手,摸清自身。” 、 、
B.以《健康秩序、健康生活》为主题的中央电视台2004年“3·15”电视宣传活动将由央视经济频道的11个栏目共同组织完成。
C.一方面是旅游线路老化、接待能力不足,另一方面是游客口味不一、经济承受能力不同.这是我国开放欧洲旅游面临的两大难题。
D.最近多名省部级高官因贪污受贿被判处死刑,人民群众无不拍手称快,但人们还在关注着检察机关对那些行贿者将如何处置?
1.下列各句中,标点符号使用正确的一句是 ( )
A.随着社会的进步,经济的发展,尤其是生活方式的改变,人类疾病谱中的高血压病、高血脂病、高血糖病--俗称“三高”的发病率急骤增高。
B.“海之梦”巡游表演.“海之旅”滨海乡情游,“海之月”沙滩赏月,“海之味”美食节等活动。把美丽的金山卫海滩打造成了休闲度假的黄金海岸。
C.我终于学会了广东话--这一事实也向所有想学外语的人证明了一点。年龄并非学习语言的障碍.只要你肯下定决心去做。
D.在申城最大的水果批发市场华中交易中心,有海南、云南瓜果、新疆葡萄、黑龙江苹果,还有浙江、安徽、山东、河南、江西、湖北等省市的水果,品种多达30余种。
20、(本小题满分16分)
已知A、B、C是直线l上的三点,向量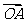 ,
, ,
, 满足
满足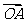 -[
-[ +2f /(1)]
+2f /(1)] +ln(x+1)
+ln(x+1) =
= .
.
(Ⅰ)求函数y=f(x)的表达式;
(Ⅱ)若x>0,证明:f(x)>;
(Ⅲ)若不等式x2≤f(x2)+m2-2bm-3时,x∈[-1,1]及b∈[-1,1]都恒成立,求实数m的取值范围.
解:(Ⅰ)∵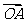 -[
-[ +2f /(1)]
+2f /(1)]  +ln(x+1)
+ln(x+1)  =
= ,
,
∴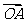 =[
=[ +2f /(1)]
+2f /(1)]  -ln(x+1)
-ln(x+1)  ,
,
由于A、B、C三点共线 即[ +2f /(1)]+[-ln(x+1)]=1…2分
+2f /(1)]+[-ln(x+1)]=1…2分
∴y=f(x)=ln(x+1)+1-2f /(1)
f /(x)=,得f /(1)=,故f(x)=ln(x+1)…………5分
(Ⅱ)令g(x)=f(x)- ,由g/(x)=-=
∵x>0,∴g/(x)>0,∴g(x)在(0,+∞)上是增函数…………8分
故g(x)>g(0)=0
即f(x)>………………………………………………10分
(Ⅲ)原不等式等价于x2-f(x2)≤m2-2bm-3
令h(x)=x2-f(x2)=x2-ln(1+x2),由h/(x)=x-=…12分
当x∈[-1,1]时,h(x)max=0,∴m2-2bm-3≥0
令Q(b)=m2-2bm-3,则
得m≥3或m≤-3……………………………………………………16分
19、(本小题满分16分)
对于函数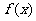 ,若存在
,若存在 ,使
,使 成立,则称
成立,则称 为
为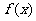 的不动点。如果函数
的不动点。如果函数 有且仅有两个不动点
有且仅有两个不动点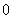 、
、 ,且
,且 。
。
(Ⅰ)求函数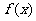 的解析式;
的解析式;
(Ⅱ)判断函数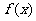 在
在 上的单调性,并证明;
上的单调性,并证明;
(Ⅲ)试判断把函数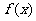 的图像作怎样的平移变换后所得函数
的图像作怎样的平移变换后所得函数 的图像关于原点对称,并说明理由。
的图像关于原点对称,并说明理由。
(Ⅰ)设
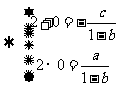 ∴
∴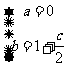 ……………………2分
……………………2分
∴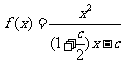
由 ……………………4分
……………………4分
又∵ ∴
∴
∴ ………………………………6分
………………………………6分
(Ⅱ)函数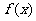 在
在 上的单调递增函数,证明略 ……………12分
上的单调递增函数,证明略 ……………12分
(Ⅲ)把函数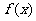 的图像依次向左、向下平移一个单位所得函数
的图像依次向左、向下平移一个单位所得函数 的图像关于原点对称。
的图像关于原点对称。
……………………………16分
18、(本小题满分16分)
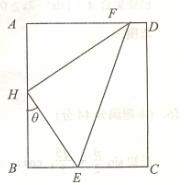 矩形ABCD中,AB=2,AD
矩形ABCD中,AB=2,AD , H是AB中点,以H为直角顶点作矩形的内接直角三角形HEF,其中E、F分别落在线段BC和线段AD上如图.记∠BHE为
, H是AB中点,以H为直角顶点作矩形的内接直角三角形HEF,其中E、F分别落在线段BC和线段AD上如图.记∠BHE为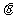 ,记
,记
 的周长为,
的周长为,
(Ⅰ)试将 表示为
表示为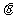 的函数;
的函数;
(Ⅱ)求 的最小值及此时的
的最小值及此时的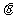 .
.
解:(1)由图知在 中,有
中,有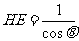 ; …………………1分
; …………………1分
在 中,有
中,有 ,
…………………2分
,
…………………2分
在 中,有
中,有 , …………………4分
, …………………4分
∴ (
( )………8分
)………8分
(2) ………………10分
………………10分
令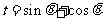 ,则
,则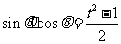 ;
;
又 ,
,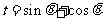

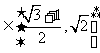 ,……13分
,……13分
∴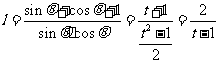
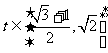
∵
∴ .……16分
.……16分
17、(本小题满分14分)
设 ,
, ,
, 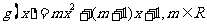 ,
,
(Ⅰ)设集合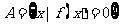 ,
, ;若
;若 ,求
,求 取值的
取值的
集合;
(Ⅱ)设集合
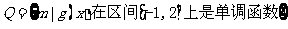 ,求
,求 .
.
解:(1)A= ;
…………………………………………1分
;
…………………………………………1分
当 时,B=
时,B= ,此时
,此时 ,∴
,∴ 适合;…………………2分
适合;…………………2分
当 时,
时,
当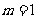 时,
时, ,此时
,此时 ,∴
,∴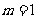 适合;………4分
适合;………4分
当 时,
时, ,又
,又 ,∴
,∴ ,……6分
,……6分
综上:实数 取值的集合为
取值的集合为 ; …………………………………7分
; …………………………………7分
(2) ,
…………………………………8分
,
…………………………………8分
当 时,
时, 满足条件,∴
满足条件,∴ 适合;…………………9分
适合;…………………9分
当 时,
时,
由题意有: …………………………11分
…………………………11分
解得 …………………………………12分
…………………………………12分
综上:Q= , ……………………………………………………13分
, ……………………………………………………13分
∴ =
= ……………………………………………………14分
……………………………………………………14分
16、 (本小题满分14分)
(本小题满分14分)
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,
AP=AB,BP=BC=2,E,F分别是PB,PC的中点.
(Ⅰ)证明:EF∥平面PAD;
(Ⅱ)证明:平面PAD⊥平面PCD;
(Ⅲ)求三棱锥E-ABC的体积V.
解:(Ⅰ)在△PBC中,E,F分别是PB,PC的中点,∴EF∥BC.
又BC∥AD,∴EF∥AD, ………………………………………2分
又∵AD 平面PAD,EF
平面PAD,EF 平面PAD,
平面PAD,
∴EF∥平面PAD. ………………………………………4分
(Ⅱ)由PA⊥平面ABCD,CD  平面ABCD,∴CD⊥PA, …………………………6分
平面ABCD,∴CD⊥PA, …………………………6分
又底面ABCD是矩形,∴CD⊥AD, 而PA, AD为平面PAD内两条相交直线,
∴CD⊥平面PAD, …………………………………………8分
又CD  平面PCD,∴平面PAD⊥平面PCD………………………………………9分
平面PCD,∴平面PAD⊥平面PCD………………………………………9分
(Ⅲ)连接AE,AC,EC,过E作EG∥PA交AB于点G,
则BG⊥平面ABCD,且EG= PA. ………………………………………11分
PA. ………………………………………11分
在△PAB中,AD=AB, PAB°,BP=2,∴AP=AB=
PAB°,BP=2,∴AP=AB= ,EG=
,EG=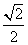 .
.
∴S△ABC= AB·BC=
AB·BC= ×
× ×2=
×2= ,
,
∴VE-ABC= S△ABC·EG=
S△ABC·EG= ×
× ×
×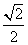 =
= .…………………………………………14分
.…………………………………………14分
15.(本小题满分14分)
在平面直角坐标系 中,已知点
中,已知点 其中
其中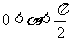 .
.
(Ⅰ)若 求证:
求证: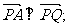
(Ⅱ)若 求
求 的值.
的值.
解:(1)(方法一)
由题设知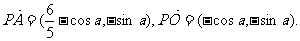 ……………………2分
……………………2分
所以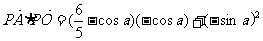
 ……………………6分
……………………6分
因为 所以
所以 故
故 ……………………7分
……………………7分
(方法二)
因为
 所以
所以 ,故
,故 ………………2分
………………2分
因此 ……………………4分
……………………4分
因为
所以
(2)因为 所以
所以
即
解得 ……………………9分
……………………9分
因为 所以
所以
因此 ……………………12分
……………………12分
从而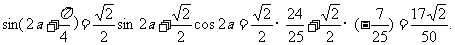 …14分
…14分
14、设定义在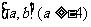 上的函数
上的函数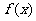 ,若函数
,若函数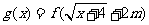 与
与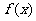 的定义域与值域都相同,则实数
的定义域与值域都相同,则实数 的取值范围为 ▲
。
的取值范围为 ▲
。
13、函数 对于任意
对于任意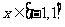 总有
总有 成立,则
成立,则 ▲
4
▲
4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com