
5.垂直于球的直径的两个平面把直径分成1∶5∶4的三段,那么这两个平面截得球得到的截面面积之比为_________.
4.一个正多面体的体积为V,它的表面一个多边形的面积为S,则此正多面体内一点到各侧面距离之和为_________.
3.在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN垂直于侧面PBC,则此正三棱锥的侧面积与底面积之比为
A.1∶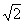 B.
B.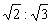
C.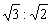 D.
D.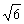 ∶1
∶1
2.正四面体的内切球和外接球的半径分别为r和R,则r∶R是
A.1∶2 B.1∶3 C.1∶4 D.1∶9
1.正方体的八个顶点中,有四个恰好为正四面体的顶点,则正方体的表面积与正四面体的表面积之比为
A.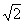 B.
B.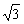 C.
C.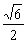 D.
D.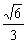
话题作文要有所创新,就应调用多种叙述方法。除以上叙事方式外,还可把文章分为时间顺序、空间顺序、逻辑顺序和意识流顺序。但无论使用何种叙述方法,其主要目的在于叙事条理清楚、层次分明。能将所选用的材料连缀成一个有机统一的整体。
例文1
童 年
沙丁鱼罐头似的公共汽车在晒得发烫的柏油路上缓慢地爬着。我--瘦瘦小小的个子在拥挤着的人群中喘不过气来。“还要多久呀?”人们烦躁而沉闷的气氛充斥着整个车厢。忽然,我看见
一位西装人士,正悄悄地把手伸入一位老人的口袋。我的第一反应就是有小偷!于是大声呼喊,一车人都回头惊悸地看着我,西装人士也恶狠狠地盯着我,随即又混入人群。我红着脸,还没到站就匆匆逃离了。仿佛那个小偷是我,我错了吗?年幼的我不懂那么多,只知道那是我心灵的选择。
我的大学
毕业考试了,我坐在考场上为未来而努力。其实,我稍稍瞥一眼就可看见邻桌的试卷,恰巧我有一题忘了。怎么办?看还是不看?我在矛盾的边缘游移。看了,也许就意味着我会有一份好工作,一个美好的前途,一个美好幸福的家庭……那就看吧!不行!我的心灵叩问着我:那是你吗?那是诚实的你吗?你不能为此失去诚实的品德呀!
可是,如果我不看,我可能就会与“成功”失之交臂,我也许将过着贫困潦倒的生活。但是,我如果那样做,我就不是忠于自我,即使我有光明的前途又怎样?
12.设函数 ,区间M=[a,b](a<b),集合N={
,区间M=[a,b](a<b),集合N={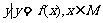 },则使M=N成立的实数对(a,b)有
( )
},则使M=N成立的实数对(a,b)有
( )
A.0个 B.1个 C.2个 D.无数多个
11.设k>1,f(x)=k(x-1)(x∈R) . 在平面直角坐标系xOy中,函数y=f(x)的图象与x轴交于A 点,它的反函数y=f -1(x)的图象与y轴交于B点,并且这两个函数的图象交于P点. 已知四边形OAPB的面积是3,则k等于 ( )
A.3 B. C. D.
10.函数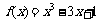 在闭区间[-3,0]上的最大值、最小值分别是( )
在闭区间[-3,0]上的最大值、最小值分别是( )
A.1,-1 B.1,-17 C.3,-17 D.9,-19
9.将一颗质地均匀的骰子(它是一种各面上分
别标有点数1,2,3,4,5,6的正方体玩具)先后抛掷3次,至少出现一次6点向上的概率是( )
A. B. C. D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com