
4.已知变量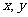 满足约束条件
满足约束条件 则
则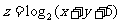 的最大值为( )
的最大值为( )
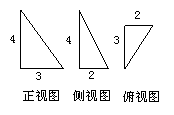 A. 2 B. 3
C.4 D.5
A. 2 B. 3
C.4 D.5
3.已知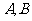 是
是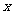 轴上不同的两点,点
轴上不同的两点,点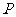 的横坐标为
的横坐标为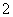 ,且|
,且|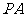 |=|
|=|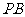 |.若直线
|.若直线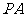 的方程为
的方程为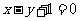 ,则直线
,则直线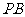 的方程为
(
)
的方程为
(
)
A. B.
B. 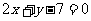 C.
C.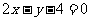 D.
D.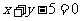
2.命题“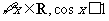 ”的否定是
( )
”的否定是
( )
A.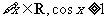 B.
B.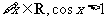
C.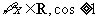 D.
D.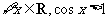
1.已知集合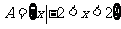 ,
,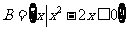 ,则
,则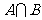 等于 (
)
等于 (
)
A.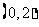 B.
B. C.
C.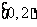 D.
D.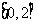
2.由n×n个边长为1的小正方形拼成的正方形棋盘中,求由若干个小方格能拼成的所有正方形的数目.
解答:如下图,根据分步计数原理,边长为k(1≤k≤n,k∈N*)的正方形共有
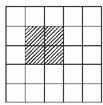
(n-k+1)(n-k+1)=(n-k+1)2(个);由分类计数原理,图形中所有正方形的数目是n2+(n-1)2+(n-2)2+…+22+12=n(n+1)·(2n+1)(个).
1.某体育彩票规定:从01至36共36个号中抽出7个号为一注,每注2元,某人想从01至10中选3个连续的号,从11至20中选2个连续的号,从21至30中选1个号,从31至36中选1个号组成一注,则这人把这种特殊要求的号买全,至少要花( )
A.3 360元 B.6 720元 C.4 320元 D.8 640元
解析:从01至10中选3个连续的号共有8种选法;
从11至20中选2个连接的号共有9种选法;
从21至30中选1个号有10种选法;从31至36中选一个号有6种选法,由分步计数原理共有8×9×10×6=4 320(注),至少需花4 320×2=8 640(元).
答案:D
10.如下图所示,三组平行线分别有m、n、k条,在此图形中
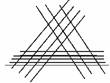
(1)共有多少个三角形?
(2)共有多少个平行四边形?
解答:(1)每个三角形与从三组平行线中各取一条的取法是一一对应的,由分步计数原理知共可构成m·n·k个三角形.
(2)每个平行四边形与从两组平行线中各取两条的取法是一一对应的,由分类和分步计数原理知共可构成CC+CC+CC个平行四边形.
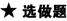
9.已知集合A={a1,a2,a3,a4},B={0,1,2,3},f是从A到B的映射.
(1)若B中每一元素都有原象,这样不同的f有多少个?
(2)若B中的元素0必无原象,这样的f有多少个?
(3)若f满足f(a1)+f(a2)+f(a3)+f(a4)=4,这样的f又有多少个?
解答:(1)显然对应是一一对应的,即为a1找象有4种方法,a2找象有3种方法,a3找象有2种方法,a4找象有1种方法,所以不同的f共有4×3×2×1=24(个).
(2)0必无原象,1,2,3有无原象不限,所以为A中每一元素找象时都有3种方法.所以不同的f共有34=81(个).
(3)分为如下四类:
第一类,A中每一元素都与1对应,有1种方法;
第二类,A中有两个元素对应1,一个元素对应2,另一个元素与0对应,有C·C=12种方法;
第三类,A中有两个元素对应2,另两个元素对应0,有C·C=6种方法;
第四类,A中有一个元素对应1,一个元素对应3,另两个元素与0对应,有C·C=12种方法.
所以不同的f共有1+12+6+12=31(个).
8.海岛上信号站的值班员总用红、黄、白三色各三面旗向附近海域出示旗语,在旗标上纵排挂,可以是一面、两面、三面,那么这样的旗语有多少种?
解答:悬挂一面旗共有3种旗语;
悬挂两面旗共有3×3=9种旗语;
悬挂三面旗共有3×3×3=27种旗语.
由分类计数原理,共有3+9+27=39种旗语.
7.8名世界网球顶级选手在上海大师赛上分成两组,每组各4人,分别进行单循环赛,每组决出前两名,再由每组的第一名与另一组的第二名进行淘汰赛,获胜者角逐冠、亚军,败者角逐第3、4名,大师赛共有________场比赛.
解析:小组赛共有2C场比赛;半决赛和决赛共有2+2=4场比赛;根据分类计数原理共有2C+4=16场比赛.
答案:16
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com