
5.设不等式2x-1>m(x -1)对满足|m|≤2的一切实数m的取值都成立。则x的取值范围是
。
-1)对满足|m|≤2的一切实数m的取值都成立。则x的取值范围是
。
4.东方旅社有100张普通客床,每床每夜收租费10元时,客床可以全部租出,若每床每夜收费提高2元,便减少10张床租出,再提高2元,又再减少10张床租出,依此变化下去,为了投资少而获利大,每床每夜应提高租金(B)
A.4元 B、6元 C、4元或6元 D、8元
3.如果实数x、y满足(x-2)2+y2=3,那么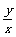 的最大值是 ( )
的最大值是 ( )
A. B.
B. C.
C. D.
D.
2.如果0<a<1,0<x≤y<1,且logax·logay=1,则xy ( )
A.有最大值,也有最小值 B.无最大值,但有最小值
C.有最大值,但无最小值 D.无最大值也无最小值
1.函数f(y)= 的最大值是
( )
的最大值是
( )
A.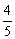 B.
B. C.
C. D.
D.
4.常见函数模型
(1)二次函数型。
(2) “对钩函数” 型
型
(3) 分段函数模型。
(4) y=N(1+p)y型及数列型
2.求函数最值的方法(求最值与求值域一般相同,最值问题更具综合性和灵活性)
(1)配方法:用于二次函数,或可通过换元法转化为二次函数的最值问题;
(2)判别式法:运用方程思想,依据二次方程有根,求出y的最值,但必须检验这个最值在定义域内有相应的x的值;
(3)不等式法:利用平均不等式求最值,注意一正二定三等;
(4)换元法:通过变量代换,化繁为简,化难为易,化未知为已知,其中三角代换是重要方法。换元后须注意新变量的取值范围;
(5)数形结合法(图象法):当一个函数图象可作时,通过图象可求其最值;
(6)单调性法:利用函数的单调性求最值;
(7)求导法:当一个函数在定义域上可导时,可据其导数求最值.
1.函数的最值的定义:函数y=f(y),定义域为A,若存在y0∈A,使得对任意的y∈A,恒有
 成立,则称
成立,则称 为函数的最小(大)值。
为函数的最小(大)值。
2.掌握解应用题的一般步骤和建模方法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com