
3.不等式恒成立问题转化为最值问题
2.用不等式求最值时要注意“=”的成立条件;
1.熟练掌握求函数最值的几种方法,并能灵活转化运用;
[例1]已知函数f(x)=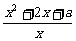 , x∈[1,+∞
, x∈[1,+∞
(1)当a=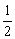 时,求函数f(x)的最小值
时,求函数f(x)的最小值
(2)若对任意x∈[1,+∞ ,f(x)>0恒成立,试求实数a的取值范围
,f(x)>0恒成立,试求实数a的取值范围
解:(1) 当a=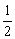 时,f(x)=x+
时,f(x)=x+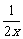 +2
+2
∵f(x)在区间[1,+∞ 上为增函数,
上为增函数,
∴f(x)在区间[1,+∞ 上的最小值为f(1)=
上的最小值为f(1)=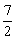
(2)解法一: 在区间[1,+∞ 上,
上,
f(x)=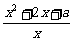 >0恒成立
>0恒成立 x2+2x+a>0恒成立
x2+2x+a>0恒成立
设y=x2+2x+a, x∈[1,+∞
∵y=x2+2x+a=(x+1)2+a-1递增,
∴当x=1时,ymin=3+a,当且仅当ymin=3+a>0时,函数f(x)>0恒成立,
故a>-3 ?
解法二:f(x)=x+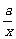 +2, x∈[1,+∞
+2, x∈[1,+∞
当a≥0时,函数f(x)的值恒为正;
当a<0时,函数f(x)递增,故当x=1时,f(x)min=3+a,
当且仅当f(x)min=3+a>0时,函数f(x)>0恒成立,故a>-3
解法分析:(1)中不能用用判别式法求最值, 对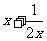 也不能用均值不等式求最值,只能用”对钩”函数的的单调性求最值.
也不能用均值不等式求最值,只能用”对钩”函数的的单调性求最值.
(2)中法一转化的很高明,法二是这一类题的一般解法。
[例2]某农产品去年各季度的市场价格如下表:
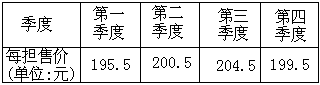
今年某公司计划按去年各季度市场价的“最佳近似值m”(m是与上表中各售价差的平方和取最小值时的值)收购该种农产品,并按每100元纳税10元(又称征税率为10个百分点),计划可收购a万担,政府为了鼓励收购公司多收购这种农产品,决定将税率降低x个百分点,预测收购量可增加2x个百分点。
(1)根据题中条件填空,m= (元/担)
(2)写出税收y(万元)与x的函数关系式;
(3)若要使此项税收在税率调节后不少于原计划税收的83.2%,试确定x的取值范围。
解:设平方和为y
(1)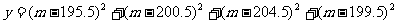
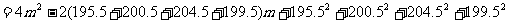
取最小值时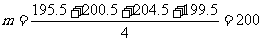 ,故应填200.
,故应填200.
(2)降低税率后的税率为(10-x)%,农产品的收购量为a(1+2x%)万担,收购总金额200·a(1+2x%),依题意,
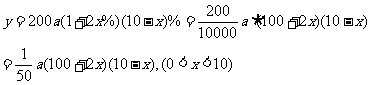
(3)原计划税收为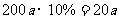 (万元),依题意,得:
(万元),依题意,得:
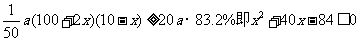 ,
,
解得: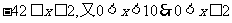
答:x的取值范围是0<x≤2.
方法提炼:理清m 的实际意义求出m;建模,解二次不等式.
[例3]某校办工厂有毁坏的房屋一幢,留有旧墙一面,其长14m,现准备利用这面旧墙,建造平面图形为矩形,面积为126m2的厂房,工程条件:(1)修1m旧墙的费用是建1m新墙的费用的25%,(2)用拆去1m旧墙的材料建1m新墙,其费用是建1m新墙费用的50%,(3)建门窗的费用与建新墙的费用相同,问:如何利用旧墙才能使建墙费用最低?
解:设利用旧墙的一面矩形边长为x,则矩形的另一面边长为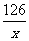
(1)利用旧墙的一段xm(x<14)为矩形的一面长,则修旧墙的费用为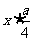 ,剩余的旧墙拆得的材料建新墙的费用为
,剩余的旧墙拆得的材料建新墙的费用为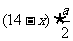 ,其余的建新墙的费用为
,其余的建新墙的费用为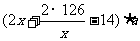
故总费用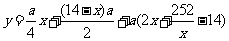
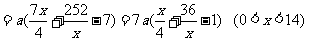
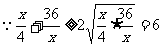 ∴当且仅当x=12时,y最小=7a(6-1)=35a
∴当且仅当x=12时,y最小=7a(6-1)=35a
(2)若利用旧墙的一面矩形边长x≥14,则修旧墙的费用为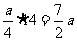 ,建新墙的费用为
,建新墙的费用为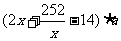 ,故总费用
,故总费用

设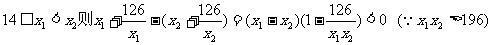
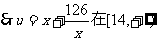 上为增函数,
上为增函数,
∴当x=14时,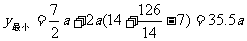
所以,采用第一种方案,利用旧墙12m为矩形的一面边长,使建墙费用最省。
特别提醒: 本题要对厂房一边长<、>14两种方案都作讨论.
[例4]某海滨浴场的岸边可以近似的看成直线,位于岸边A处的救生员发现海中B处有人求救,若救生员在岸边的行进速度为6米/秒,在海中的行进速度2米/秒,在AD上找一落点C,使救生员从A到B的时间最短,并求出最短时间。
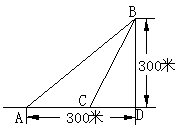 解:
解: 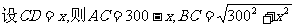 ,则从A经C到B的时间为t,
,则从A经C到B的时间为t,
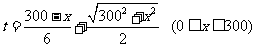
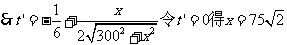
 因此点C应选沿岸边AD距D点
因此点C应选沿岸边AD距D点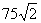 米处,才能使救生员从A经C到B所用的时间最短为
米处,才能使救生员从A经C到B所用的时间最短为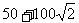 秒
秒
法二:设∠DBC=α则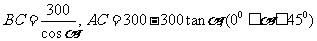 ,用时
,用时
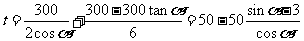
记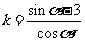 ,它表示点(cosα,sinα)和(0,3)连线的斜率,结合图形知当连线与圆弧
,它表示点(cosα,sinα)和(0,3)连线的斜率,结合图形知当连线与圆弧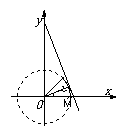 相切时k 最大,t最小,y=ky+3代入y2+y2=1,Δ=0,得
相切时k 最大,t最小,y=ky+3代入y2+y2=1,Δ=0,得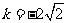 ,
,
此时 ,
, 最小.
最小.
解法研讨:法一:以CD长为自变量建模,导数法求最值;法二:以∠DBC为自变量建模,方法更具灵活性.
[研讨.欣赏]
(2006湖南)对1个单位质量的含污物体进行清洗,
清洗前其清洁度(含污物体的清洁度定义为:1-污物质量÷物体质量(含污物))为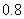 , 要求清洗完后的清洁度为
, 要求清洗完后的清洁度为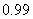 . 有两种方案可供选择, 方案甲: 一次清洗; 方案乙: 分两次清洗. 该物体初次清洗后受残留水等因素影响, 其质量变为a(1≤a≤3). 设用
. 有两种方案可供选择, 方案甲: 一次清洗; 方案乙: 分两次清洗. 该物体初次清洗后受残留水等因素影响, 其质量变为a(1≤a≤3). 设用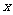 单位质量的水初次清洗后的清洁度是c=
单位质量的水初次清洗后的清洁度是c=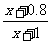 , (0.8<c<0.99,
x>a-1), 用
, (0.8<c<0.99,
x>a-1), 用 单位质量的水第二次清洗后的清洁度是
单位质量的水第二次清洗后的清洁度是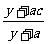 ,
,
(Ⅰ)分别求出方案甲以及c=0.95时方案乙的用水量, 并比较哪一种方案用水量较少;
(Ⅱ)若采用方案乙, 当a为某定值时, 如何安排初次与第二次清洗的用水量, 使总用水量最小? 并讨论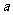 取不同数值时对最少总用水量多少的影响.
取不同数值时对最少总用水量多少的影响.
解:(Ⅰ)设方案甲与方案乙的用水量分别为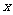 与
与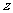 ,由题设有
,由题设有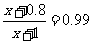 ,解得
,解得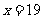
由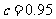 得方案乙初次用水量为3,第二次用水量
得方案乙初次用水量为3,第二次用水量 满足方程
满足方程
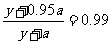 ,解得
,解得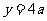 ,故
,故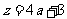
即两种方案的用水量分别为19与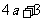 。
。
因为当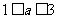 时,
时, ,即
,即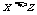 ,
,
故方案乙的用水量较少
(Ⅱ)设初次与第二次清晰的用水量分别为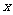 与
与 ,类似(Ⅰ)得
,类似(Ⅰ)得
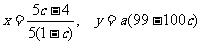 (*)
(*)
于是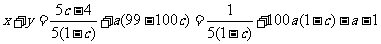
当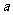 为定值时,
为定值时,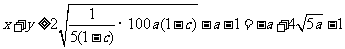
当且仅当
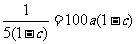 时等号成立,此时
时等号成立,此时 (不合题意,舍去)
(不合题意,舍去)
或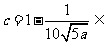 (0.8,0.99)
(0.8,0.99)
将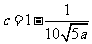 代入(*)式得
代入(*)式得
故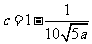 时总用水量最少,此时第一次与第二次用水量分别为
时总用水量最少,此时第一次与第二次用水量分别为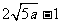 与
与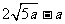 ,最少总用水量是
,最少总用水量是
当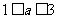 时,
时, ,故
,故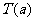 是增函数(也可以用二次函数的单调性判断)。这说明,随着
是增函数(也可以用二次函数的单调性判断)。这说明,随着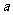 的值的增加,最少总用水量增加。
的值的增加,最少总用水量增加。
6.设x=cosα,y=cosβ,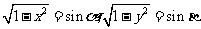
由已知x,y不能取负值,否则,若x<0,则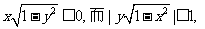 则已知不成立,故x,y均不小于0.
则已知不成立,故x,y均不小于0.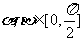
∴cosαsinβ+cosβsinα=1,α+β=π/2,x+y=cosα+sinα最小值是1;
7 t=
t=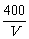 +16×(
+16×(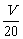 )2/V=
)2/V=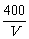 +
+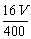 ≥2
≥2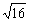 =8
=8
5.即f(m)=(x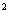 -1)m-(2x-1)<0在[-2,2] 恒成立, 则f(2)<0且f(-2)<0解得x∈(
-1)m-(2x-1)<0在[-2,2] 恒成立, 则f(2)<0且f(-2)<0解得x∈(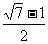 ,
,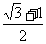 );
);
4. 设提价2x元,则获利y=(10+x)(100-10x)= -20(x2-5x-50),x=2或3时最大,x=3时投资小;
3.数形结合;
2.设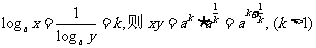 .
.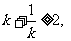
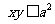 ,当k=1,即x=y=a时取等号.k+1/k无最大值,xy无最小值;
,当k=1,即x=y=a时取等号.k+1/k无最大值,xy无最小值;
6.若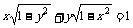 ,则y+y的最小值是_____________.
,则y+y的最小值是_____________.
7 一批货物随17列货车从A市以V千米/小时匀速直达B市,已知两地铁路线长400千米,为了安全,两列货车间距离不得小于(
一批货物随17列货车从A市以V千米/小时匀速直达B市,已知两地铁路线长400千米,为了安全,两列货车间距离不得小于(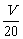 )2千米 ,那么这批物资全部运到B市,最快需要_________小时(不计货车的车身长)
)2千米 ,那么这批物资全部运到B市,最快需要_________小时(不计货车的车身长)
简答提示:1-4.DCDB; 1.配方法分母≥3/4, 再由不等式法;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com