
2.熟悉角的变换技巧,注意倍角的相对性, 时时注意角的范围的讨论.
1.要熟练推证公式理清公式间的推导线索(建议自己推证一遍所有公式)、熟悉公式的正用逆用和变形应用,公式应用讲究一个“活”字.
3.注意隐含条件sinγ>0,否则产生增根.
[例4]已知α为第二象限角,cos +sin
+sin =-
=-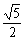 ,求sin
,求sin -cos
-cos 和sin2α+cos2α的值.
和sin2α+cos2α的值.
解:由cos +sin
+sin =-
=-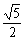 平方得
平方得
1+2sin cos
cos =
=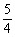 ,
,
即sinα=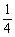 ,cosα=-
,cosα=-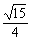 .
.
此时kπ+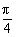 <
< <kπ+
<kπ+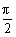 .
.
∵cos +sin
+sin =-
=-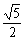 <0,
<0,
sin cos
cos =
=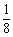 >0,
>0,
∴cos <0,sin
<0,sin <0.
<0.
∴ 为第三象限角.
为第三象限角.
∴2kπ+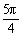 <
< <2kπ+
<2kπ+ ,k∈Z.
,k∈Z.
∴sin <cos
<cos ,
,
即sin -cos
-cos <0.
<0.
∴sin -cos
-cos =-
=-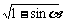 =-
=-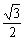 ,
,
sin2α+cos2α=2sinαcosα+1-2sin2α=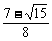 .
.
[研讨.欣赏](2005湖南)已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A、B、C的大小.
解法一 由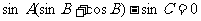 得
得
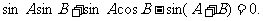
所以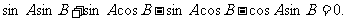 即
即
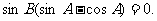
因为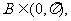 所以
所以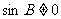 ,从而
,从而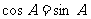
由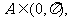 知
知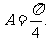 从而
从而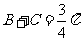 由
由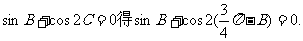
即
由此得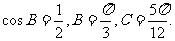 所以
所以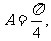
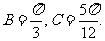
解法二:由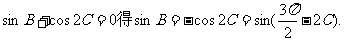
由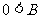 、
、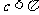 ,所以
,所以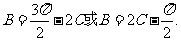 即
即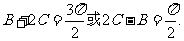
由 得
得 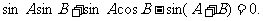
所以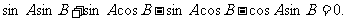
即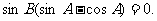 因为
因为 ,所以
,所以
由 从而
从而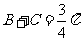 ,知B+2C=
,知B+2C=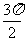 不合要求.
不合要求.
再由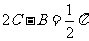 ,得
,得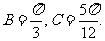 所以
所以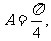
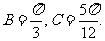
2.解题关键有二:一是消元γ,二是凑差角余弦公式,倒用.
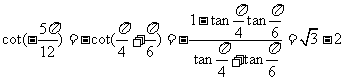
[例1]求值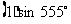 ;
; 
解(1):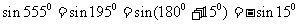
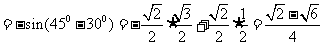
(2)
[例2](1)设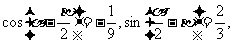
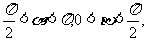
(2) 已知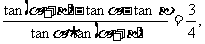 且
且 求
求
解:(1) 因为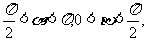 所以
所以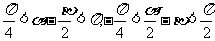
所以 ,
,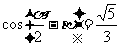 ,
,
所以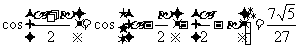
故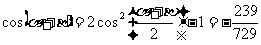
(2) 原式=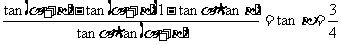
又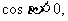 所以
所以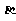 为第三象限角,所以
为第三象限角,所以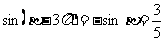
◆思路方法: 1.三角函数变形着眼于两点:一是寻找角的变换,二是分析函数式的结构与联系,合理利用公式。
2.涉及α+β、α及β的正切和差与积,通常用正切公式的变形公式。
[例3] 已知α、β、γ∈(0,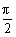 ),sinα+sinγ=sinβ,cosβ+cosγ=cosα,求β-α的值.
),sinα+sinγ=sinβ,cosβ+cosγ=cosα,求β-α的值.
解:由已知,得sinγ=sinβ-sinα,cosγ=cosα-cosβ.
平方相加得
(sinβ-sinα)2+(cosα-cosβ)2=1.
∴-2cos(β-α)=-1.∴cos(β-α)=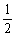 .
.
∴β-α=± .
.
∵sinγ=sinβ-sinα>0,∴β>α.∴β-α= .
.
◆解法点粹:1.求角一般要先求出它的一个三角函数值;
6. 利用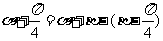 …答案:
…答案:
5.原式= ,答案:2
,答案:2
4.画图知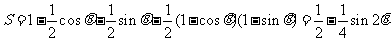 ,
, 时最大.
时最大.
3.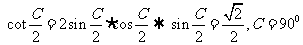 …
…
2.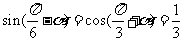 ,
,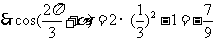 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com