
7. 已知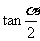 =2,求
=2,求
(I)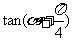 的值; (II)sin2α+sin2α+cos2α的值.
的值; (II)sin2α+sin2α+cos2α的值.
解:(I)∵
tan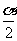 =2, ∴
=2, ∴ 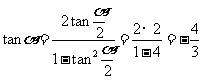 ;
;
所以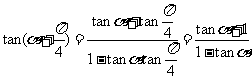 =
=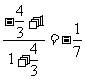 ;
;
(II)sin2α+sin2α+cos2α=sin2α+sin2α+cos2α-sin2α
=2sinαcosα+cos2α
=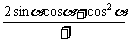 =
=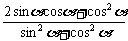
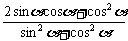 =
= =1.
=1.
6.由已知得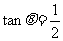 ,sin2θ-2cos2θ=
,sin2θ-2cos2θ=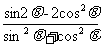 =
=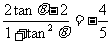
法二:sin2θ-2cos2θ=sin2θ-cos2θ-1=-cos(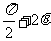 )-sin(
)-sin(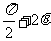 )-1
)-1
=
[解答题]
5.由已知得sinα=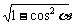 =
= ,tan
,tan =
=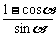 =
=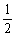 .
.
法二:tan =
=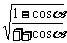 =
=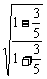 =
=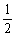 .
.
6.已知tan(45°+θ)=3,则sin2θ-2cos2θ=_______
简答.提示:1-3. ABC;4. -
5. (2005春上海)若cosα=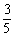 ,且α∈(0,
,且α∈(0,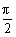 ),则tan
),则tan =_______
=_______
4. (2006陕西)cos43°cos77°+sin43°cos167°的值为
3.(全国卷Ⅲ)设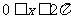 ,且
,且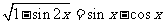 ,则
( )
,则
( )
A. 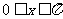 B.
B. 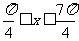 C.
C. 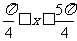 D.
D. 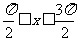
[填空题]
2.化简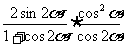 =
( )
=
( )
(A) 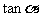 (B)
(B) 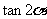 (C)
1
(D)
(C)
1
(D)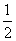
1.满足cosαcosβ=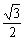 +sinαsinβ的一组α、β的值是
( )
+sinαsinβ的一组α、β的值是
( )
A.α=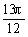 ,β=
,β=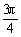 B.α=
B.α=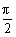 ,β=
,β=
C.α=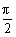 ,β=
,β=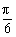 D.α=
D.α= ,β=
,β=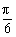
3.掌握利用和、差、倍角公式化简、求值和证明三角恒等式方法和技巧。
同步练习 4.2 和、差、倍角的三角函数
[选择题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com