
3.判断复合命题的真假的方法-真值表:“非p”形式的复合命题真假与p的 当p与q都真时,p且q形式的复合命题 ,其他情形 ;当p与q都 时,“p或q”复合形式的命题为假,其他情形 .
2.逻辑联结词有 ,不含 的命题是简单命题.
由 的命题是复合命题.复合命题的构成形式有三种: ,(其中p,q都是简单命题).
1. 可以 的语句叫做命题.命题由 两部分构成;
命题有 之分;数学中的定义、公理、定理等都是 命题.
13. (Ⅰ)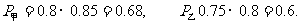
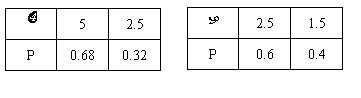 (Ⅱ)解:随机变量
(Ⅱ)解:随机变量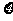 、
、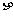 的分别列是
的分别列是

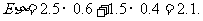
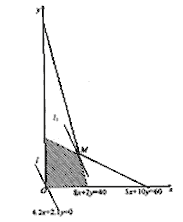 (Ⅲ)解:由题设知
(Ⅲ)解:由题设知 目标函数为
目标函数为 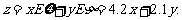
作出可行域(如图):
作直线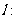
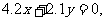
将l向右上方平移至l1位置时,直线经过可行域上
的点M点与原点距离最大,此时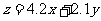
取最大值. 解方程组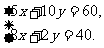
得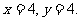 即
即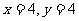 时,z取最大值,z的最大值为25.2 .
时,z取最大值,z的最大值为25.2 .
12.P(ξ=0)=P(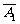
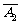
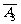 )=0.9×0.8×0.7=0.504;
)=0.9×0.8×0.7=0.504;
P(ξ=1)=P(A1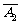
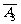 )+P(
)+P(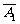 A2
A2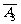 )+P(
)+P(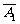
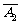 A3)=0.1×0.8×0.7+0.9×0.2×0.7+0.9×0.8×0.3=0.398;
A3)=0.1×0.8×0.7+0.9×0.2×0.7+0.9×0.8×0.3=0.398;
P(ξ=2)=P(A1A2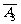 )+P(A1
)+P(A1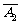 A3)+P(
A3)+P(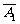 A2A3)=0.1×0.2×0.7+0.1×0.8×0.3+0.9×0.2×0.3=0.092;
A2A3)=0.1×0.2×0.7+0.1×0.8×0.3+0.9×0.2×0.3=0.092;
P(ξ=3)=P(A1A2A3)=0.1×0.2×0.3=0.006.
∴Eξ=1×0.398+2×0.092+3×0.006=0.6,
Dξ=Eξ2-(Eξ)2=1×0.398+4×0.092+9×0.006-0.62=0.82-0.36=0.46.
11. P(ξ=5)=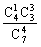 =
=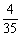 ,
,
P(ξ=6)=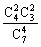 =
=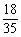 ,P(ξ=7)=
,P(ξ=7)=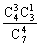 =
= ,
,
P(ξ=8)=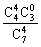 =
=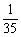 ,Eξ=5×
,Eξ=5×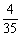 +6×
+6×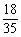 +7×
+7× +8×
+8×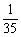 =
=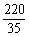 =
=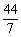 .
.
10.成绩的期望为Eη=E(2ξ)=2Eξ=2×50×0.8=80(分);
成绩的标准差为ση=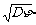 =
=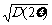 =
=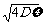 =2
=2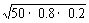 =4
=4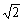 ≈5.7(分).
≈5.7(分).
14. (辽宁卷)某工厂生产甲、乙两种产品,每种产品都是经过第一和第二工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级.对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品.
(辽宁卷)某工厂生产甲、乙两种产品,每种产品都是经过第一和第二工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级.对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品.
(Ⅰ)已知甲、乙两种产品每一道工序的加工结果为A级的概率如表一所示,分别求生产出的甲、乙产品为一等品的概率P甲、P乙;
(Ⅱ)已知一件产品的利润如表二所示,用ξ、η分别表示一件甲、乙产品的利润,在(I)的条件下,求ξ、η的分布列及Eξ、Eη;
(Ⅲ)已知生产一件产品需用的工人数和资金额如表三所示.该工厂有工人40名,可用资金60万元.设x、y分别表示生产甲、乙产品的数量,在(II)的条件下,x、y为何值时, 最大?最大值是多少?(解答时须给出图示)
最大?最大值是多少?(解答时须给出图示)
离散型随机变量的期望值和方差答案
1-6. BCBAAC
7. 乙 8. 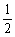 ; 5. 9. 1.2.
; 5. 9. 1.2.
13.将数字1,2,3,4任意排成一列,如果数字k恰好出现在第k个位置上,则称之为一个巧合,求巧合数的数学期望.
12.一台设备由三大部件组成,在设备运转中,各部件需要调整的概率相应为0.10,0.20和0.30.假设各部件的状态相互独立,以ξ表示同时需要调整的部件数,试求ξ的数学期望Eξ和方差Dξ.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com