
11.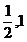 12.
12.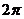
9.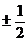 10.
10.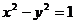
1—5 CACBB 6—8 DDA
20.(本小题满分13分)
设M是由满足下列条件的函数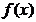 构成的集合:“①方程
构成的集合:“①方程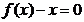 有实数根;
有实数根;
②函数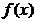 的导数
的导数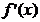 满足
满足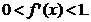 ”
”
(I)判断函数 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(II)集合M中的元素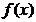 具有下面的性质:若
具有下面的性质:若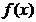 的定义域为D,则对于任意[m,n]
的定义域为D,则对于任意[m,n]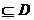 ,都存在
,都存在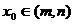 ,使得等式
,使得等式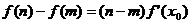 成立。试用这一性质证明:方程
成立。试用这一性质证明:方程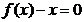 只有一个实数根;
只有一个实数根;
(III)设x1是方程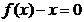 的实数根,求证:对于
的实数根,求证:对于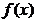 定义域中任意的x2,x3,当
定义域中任意的x2,x3,当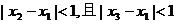 时,有
时,有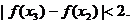
广州市东风中学2010-2011年度高三综合训练(8)
19.(本小题满分14分)
已知直线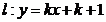 ,抛物线
,抛物线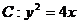 ,定点M(1,1)。
,定点M(1,1)。
(I)当直线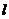 经过抛物线焦点F时,求点M关于直线
经过抛物线焦点F时,求点M关于直线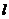 的对称点N的坐标,并判断点N 是否在抛物线C上;
的对称点N的坐标,并判断点N 是否在抛物线C上;
(II)当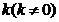 变化且直线
变化且直线 与抛物线C有公共点时,设点P(a,1)关于直线
与抛物线C有公共点时,设点P(a,1)关于直线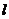 的对称点为Q(x0,y0),求x0关于k的函数关系式
的对称点为Q(x0,y0),求x0关于k的函数关系式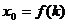 ;若P与M重合时,求
;若P与M重合时,求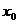 的取值范围。
的取值范围。
18.(本小题满分13分)
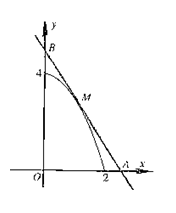
如图,已知M是函数 的图像C上一点,过M点作曲线C的切线与x轴、y轴分别交于点A,B,O是坐标原点,求△AOB面积的最小值。
的图像C上一点,过M点作曲线C的切线与x轴、y轴分别交于点A,B,O是坐标原点,求△AOB面积的最小值。
17.(本小题满分13分)
某会议室用3盏灯照明,每盏灯各使用节能灯棍一只,且型号相同。假定每盏灯能否正常照明只与灯棍的寿命有关,该型号的灯棍寿命为1年以上的概率为0.8,寿命为2年以上的概率为0.3,从使用之日起每满1年进行一次灯棍更换工作,只更换已坏的灯棍,平时不换。
(I)在第一次灯棍更换工作中,求不需要更换灯棍的概率;
(II)在第二次灯棍更换工作中,对其中的某一盏灯来说,求该灯需要更换灯棍的概率;
(III)设在第二次灯棍更换工作中,需要更换的灯棍数为ξ,求ξ的分布列和期望。
16.(本小题满分14分)
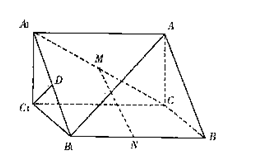 如图,直三棱柱ABC—A1B1C1的底面积是等腰直角三角形,∠A1B1C1=90°,A1C1=1,AA1=
如图,直三棱柱ABC—A1B1C1的底面积是等腰直角三角形,∠A1B1C1=90°,A1C1=1,AA1=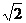 ,N、M分别是线段B1B、AC1的中点。
,N、M分别是线段B1B、AC1的中点。
(I)证明:MN//平面ABC;
(II)求A1到平面AB1C1的距离
(III)求二面角A1—AB1—C1的大小。
15.(本小题满分13分)
如图,是函数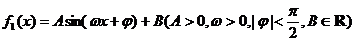 在同一个周期内的图像。
在同一个周期内的图像。
(I)求函数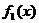 的解析式;
的解析式;
(II)将函数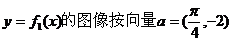 平移,得到函数
平移,得到函数
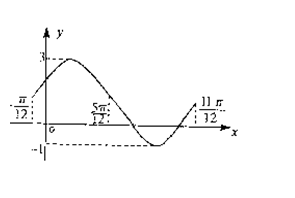
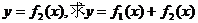 的最大值,并求此时自变量x的集合。
的最大值,并求此时自变量x的集合。
14.定义“和常数列”:在一个数列中,如果每一项与它的后一项和都为同一个常数,那么这个数列叫做常数列,这个常数叫做该数列的和常。已知数列{an}是和常数列,且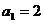 ,和常为5,那么
,和常为5,那么 的值为 ;若n为偶数,则这个数的前n项和Sn的计算公式为 。
的值为 ;若n为偶数,则这个数的前n项和Sn的计算公式为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com