
18. (本小题满分15分)某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站. 记P到三个村庄的距离之和为y.
(本小题满分15分)某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站. 记P到三个村庄的距离之和为y.
(1)设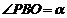 ,把y表示成
,把y表示成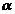 的函数关系式;
的函数关系式;
(2)变电站建于何处时,它到三个小区的距离之和最小?
[解](1)在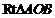 中,
中,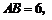 所以
所以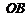 =OA=
=OA=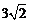 .所以
.所以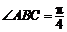
由题意知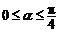 . ……………………2分
. ……………………2分
所以点P到A、B、C的距离之和为
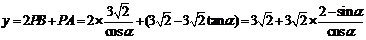 . ……………………6分
. ……………………6分
故所求函数关系式为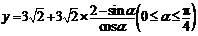 . ……………………7分
. ……………………7分
(2)由(1)得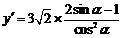 ,令
,令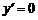 即
即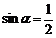 ,又
,又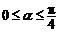 ,从而
,从而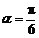 . ……………………9分.
. ……………………9分.
当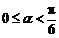 时,
时,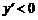 ;当
;当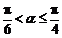 时,
时, 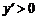 .
.
所以当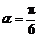 时,
时,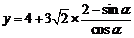 取得最小值, ………………… 13分
取得最小值, ………………… 13分
此时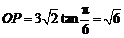 (km),即点P在OA上距O点
(km),即点P在OA上距O点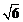 km处.
km处.
[答]变电站建于距O点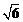 km处时,它到三个小区的距离之和最小. ………… 15分
km处时,它到三个小区的距离之和最小. ………… 15分
17.(本小题满分15分)设等差数列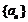 的前
的前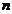 项和为
项和为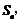 且
且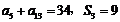 .
.
(1)求数列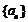 的通项公式及前
的通项公式及前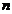 项和公式;
项和公式;
(2)设数列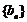 的通项公式为
的通项公式为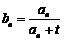 ,问: 是否存在正整数t,使得
,问: 是否存在正整数t,使得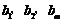
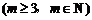 成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
[解](1)设等差数列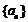 的公差为d. 由已知得
的公差为d. 由已知得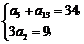 ……………………2分
……………………2分
即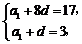 解得
解得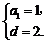 ……………………4分.故
……………………4分.故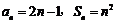 . ………6分
. ………6分
(2)由(1)知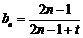 .要使
.要使 成等差数列,必须
成等差数列,必须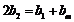 ,即
,即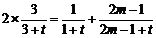 ,……8分.整理得
,……8分.整理得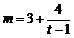 , …………… 11分
, …………… 11分
因为m,t为正整数,所以t只能取2,3,5.当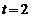 时,
时,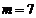 ;当
;当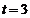 时,
时,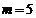 ;当
;当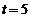 时,
时,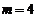 .
.
故存在正整数t,使得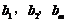 成等差数列. ………………… 15分
成等差数列. ………………… 15分
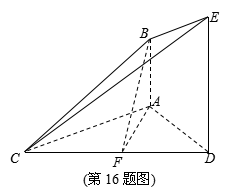
16.(本小题满分14分)如图,已知AB⊥平面ACD,DE⊥平面ACD,AC=AD,DE=2AB,F为CD的中点.
(1) 求证:AF∥平面BCE;
(2) 求证:平面BCE⊥平面CDE.
[证明](1)因为AB⊥平面ACD,DE⊥平面ACD,
所以AB∥DE.
取CE的中点G,连结BG、GF,因为F为 的中点,
的中点,
所以GF∥ED∥BA, GF=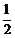 ED=BA,
ED=BA,
从而ABGF是平行四边形,于是AF∥BG. ……………………4分
因为AF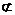 平面BCE,BG
平面BCE,BG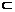 平面BCE,所以AF∥平面BCE. ……………………7分
平面BCE,所以AF∥平面BCE. ……………………7分
(2)因为AB⊥平面ACD,AF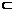 平面ACD,
平面ACD,
所以AB⊥AF,即ABGF是矩形,所以AF⊥GF. ……………………9分
又AC=AD,所以AF⊥CD. ………………… 11分
而CD∩GF=F,所以AF⊥平面GCD,即AF⊥平面CDE.
因为AF∥BG,所以BG⊥平面CDE.
因为BG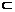 平面BCE,所以平面BCE⊥平面CDE. ………………… 14分
平面BCE,所以平面BCE⊥平面CDE. ………………… 14分
15.(本小题满分14分)在△ABC中,a,b,c分别是角A、B、C所对的边,且b2=ac,向量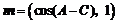 和
和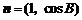 满足
满足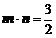 .(1)求
.(1)求 的值;(2)求证:三角形ABC为等边三角形.
的值;(2)求证:三角形ABC为等边三角形.
[解](1)由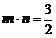 得,
得,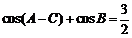 , ……………………2分
, ……………………2分
又B=π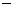 (A+C),得cos(A
(A+C),得cos(A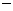 C)
C)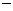 cos(A+C)=
cos(A+C)= , ……………………4分
, ……………………4分
即cosAcosC+sinAsinC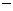 (cosAcosC
(cosAcosC sinAsinC)=
sinAsinC)=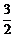 ,所以sinAsinC=
,所以sinAsinC= . ……………6分
. ……………6分
[证明](2)由b2=ac及正弦定理得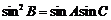 ,故
,故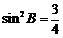 . ……………8分
. ……………8分
于是 ,所以
,所以 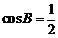 或
或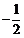 . 因为cosB =
. 因为cosB =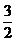
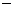 cos(A
cos(A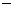 C)>0, 所以
C)>0, 所以  ,故
,故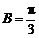 . ………………… 11分
. ………………… 11分
由余弦定理得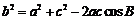 ,即
,即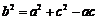 ,又b2=ac,所以
,又b2=ac,所以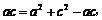 得a=c.
得a=c.
 因为
因为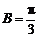 ,所以三角形ABC为等边三角形. ………………… 14分
,所以三角形ABC为等边三角形. ………………… 14分
11.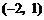 ; 12.4; 13.
; 12.4; 13.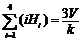 ; 14.0.
; 14.0.
6.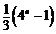 ; 7.
; 7.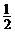 ; 8.90; 9.10; 10.①③④ ;
; 8.90; 9.10; 10.①③④ ;
1.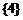 ; 2.
; 2. ; 3.2; 4.
; 3.2; 4.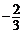 ; 5.
; 5.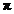 ;
;
14.在平面直角坐标系xOy中,设直线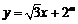 和圆
和圆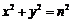 相切,其中m,
相切,其中m,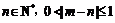 ,若函数
,若函数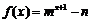 的零点
的零点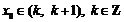 ,则k= ▲ .
,则k= ▲ .
[填空题答案]
13.设面积为S的平面四边形的第i条边的边长记为ai(i=1,2,3,4),P是该四边形内任意一点,P点到第i条边的距离记为hi,若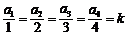 , 则
, 则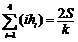 .类比上述结论,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),Q是该三棱锥内的任意一点,Q点到第i个面的距离记为Hi,则相应的正确命题是:若
.类比上述结论,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),Q是该三棱锥内的任意一点,Q点到第i个面的距离记为Hi,则相应的正确命题是:若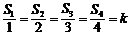 ,则 ▲ .
,则 ▲ .
12.已知椭圆的中心在坐标原点,焦点在x轴上,以其两个焦点和短轴的两个端点为顶点的
四边形是一个面积为4的正方形,设P为该椭圆上的动点,C、D的坐标分别是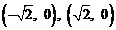 ,则PC·PD的最大值为 ▲ .
,则PC·PD的最大值为 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com