
5.对于多细胞生物而言,下列有关细胞生命历程的说法,正确的是
A.缺氧导致脑细胞死亡是细胞坏死
B.细胞癌变是所有细胞都要经历的一个阶段
C.皮肤上的老年斑是细胞凋亡的产物
D.人体各种组织细胞的衰老是同步进行的
4.某同学用下图所示实验装置测定果蝇幼虫的呼吸速率。实验所用毛细管横截面积为1mm2,实验开始时,打开软管夹,将装置放入25℃水浴中,10min后关闭软管夹,随后每隔5min记录一次毛细管中液滴移动的位置,结果如下表所示。下列分析中,正确的是
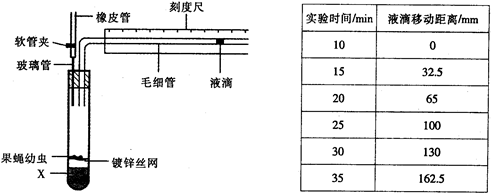
A.图中X为NaOH溶液,软管夹关闭后液滴将向右移动
B.在20min-30min内氧气的平均吸收速率为6.5mm3/min
C.如将X换为清水,并将试管充入N2即可测定果蝇幼虫无氧呼吸速率
D.增设的对照实验只将装置中的X换成清水,并将该装置置于相同的环境中
3.下图表示同一生物体内不同时期的细胞分裂图,相关说法不正确的是
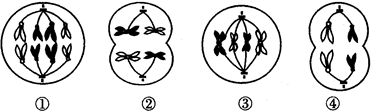
A.处于有丝分裂过程中的细胞是①和③
B.一般情况下,正在发生等位基因分离的是细胞②
C.细胞③中染色体、染色单体、核DNA数量之比为1:2:2
D.细胞③和细胞④所示过程不可能发生在同一器官中
2.下列关于细胞结构与功能的叙述,不正确的是
A.核膜上的核孔便于细胞核和细胞质之间交流大分子物质
B.成熟植物细胞通过渗透作用吸水与液泡、细胞膜等结构有关
C.心肌细胞中的线粒体数量较多与细胞消耗能量较多有关
D.细胞内各种生物膜在结构上有联系,在功能上没有联系
1.下列都含有氮元素的一组物质是
A.脱氧核糖和脱氧核糖核酸 B.胰岛素和核酸核酸
C.丙酮酸和丙氨酸 D.脂肪和脂肪酶
23.如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,
AB=BC=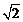 ,BB1=3,D为A1C1的中点,F在线段AA1上.
,BB1=3,D为A1C1的中点,F在线段AA1上.
(1)AF为何值时,CF⊥平面B1DF?
(2)设AF=1,求平面B1CF与平面ABC所成的锐二面角的余弦值.
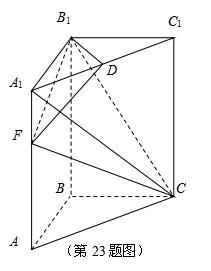 [解] (1)因为直三棱柱ABC-A1B1C1中,
[解] (1)因为直三棱柱ABC-A1B1C1中,
BB1⊥面ABC,∠ABC=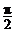 .
.
以B点为原点,BA、BC、BB1分别为x、y、z轴建立如图所示空间直角坐标系.
因为AC=2,∠ABC=90º,所以AB=BC=,
 从而B(0,0,0),A
从而B(0,0,0),A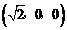 ,C
,C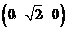 ,B1(0,0,3),A1
,B1(0,0,3),A1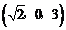 ,C1
,C1 ,D
,D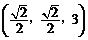 ,E
,E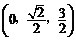 .
.
所以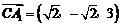 ,
,
设AF=x,则F(,0,x),
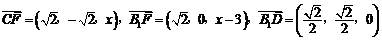 .
.
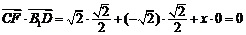 ,所以
,所以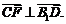
要使CF⊥平面B1DF,只需CF⊥B1F.
由 =2+x(x-3)=0,得x=1或x=2,
=2+x(x-3)=0,得x=1或x=2,
故当AF=1或2时,CF⊥平面B1DF.……………… 5分
(2)由(1)知平面ABC的法向量为n1=(0,0,1).
设平面B1CF的法向量为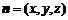 ,则由
,则由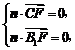 得
得
令z=1得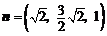 ,
,
所以平面B1CF与平面ABC所成的锐二面角的余弦值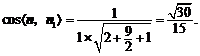
………………… 10分
22.动点P在x轴与直线l:y=3之间的区域(含边界)上运动,且到点F(0,1)和直线l的距离之和为4.
(1)求点P的轨迹C的方程;
(2)过点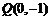 作曲线C的切线,求所作的切线与曲线C所围成区域的面积.
作曲线C的切线,求所作的切线与曲线C所围成区域的面积.
[解](1)设P(x,y),根据题意,得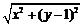 +3-y=4,化简,得y=
+3-y=4,化简,得y=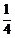 x2(y≤3).
x2(y≤3).
…………………4分
(2)设过Q的直线方程为y=kx-1,代入抛物线方程,整理得x2-4kx+4=0.
由△=16k2-16=0.解得k=±1.
于是所求切线方程为y=±x-1(亦可用导数求得切线方程).
切点的坐标为(2,1),(-2,1).
由对称性知所求的区域的面积为S=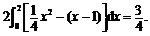 ………………… 10分
………………… 10分
21.[选做题]在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
A.选修4—1 几何证明选讲
如图,AB是⊙O的直径,C、F为⊙O上的点,且CA平分∠BAF,过点C作CD⊥AF
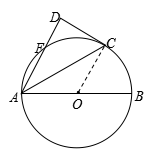 交AF的延长线于点D. 求证:DC是⊙O的切线.
交AF的延长线于点D. 求证:DC是⊙O的切线.
[证明]连结OC,所以∠OAC=∠OCA.
又因为CA平分∠BAF,所以∠OAC=∠FAC,
于是∠FAC=∠OCA,所以OC//AD.
又因为CD⊥AF,所以CD⊥OC,
故DC是⊙O的切线. ………………… 10分
B.选修4—2 矩阵与变换
变换T是绕坐标原点逆时针旋转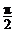 的旋转变换,求曲线
的旋转变换,求曲线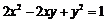 在变换T作用
在变换T作用
下所得的曲线方程.
[解]变换T所对应变换矩阵为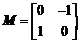 ,设
,设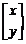 是变换后图像上任一点,与之对应的变换前的点是
是变换后图像上任一点,与之对应的变换前的点是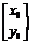 ,则
,则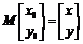 ,即
,即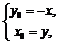 ,代入
,代入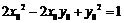 ,
,
即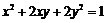 ,
,
所以变换后的曲线方程为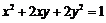 . ………………… 10分
. ………………… 10分
C.选修4—4 参数方程与极坐标(本题满分10分)
已知圆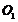 和圆
和圆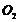 的极坐标方程分别为
的极坐标方程分别为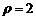 ,
,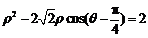 .
.
(1)把圆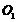 和圆
和圆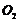 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程.
[解](1)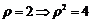 ,所以
,所以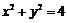 ;因为
;因为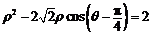 ,
,
所以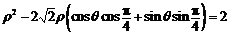 ,所以
,所以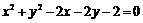 . ………5分
. ………5分
(2)将两圆的直角坐标方程相减,得经过两圆交点的直线方程为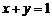 .
.
化为极坐标方程为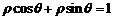 ,即
,即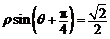 . ………………… 10分
. ………………… 10分
D.选修4—5 不等式证明选讲(本题满分10分)
已知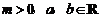 ,求证:
,求证: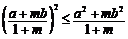 .
.
[解]因为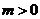 ,所以
,所以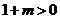 ,所以要证
,所以要证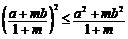 ,
,
即证 , 即证
, 即证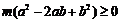 ,
,
即证 ,而
,而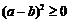 显然成立,故
显然成立,故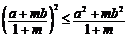 .…………… 10分
.…………… 10分
[必做题]第22题、第23题,每题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
20.(本小题满分16分)
已知二次函数g(x)对任意实数x都满足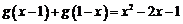 ,且
,且 .令
.令
 .
.
(1)求 g(x)的表达式;
(2)若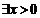 使
使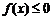 成立,求实数m的取值范围;
成立,求实数m的取值范围;
(3)设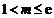 ,
,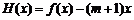 ,
,
证明:对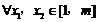 ,恒有
,恒有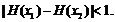
[解] (1)设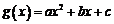 ,于是
,于是
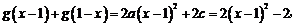 所以
所以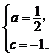
又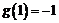 ,则
,则 .所以
.所以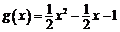 . ……………………4分
. ……………………4分
(2)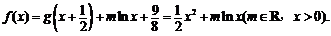
当m>0时,由对数函数性质,f(x)的值域为R;
当m=0时, 对
对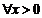 ,
,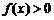 恒成立; ……………………6分
恒成立; ……………………6分
当m<0时,由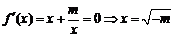 ,列表:
,列表:
| x | 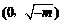 | 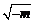 | 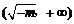 |
 | - | 0 | + |
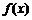 | 减 | 极小 | 增 |
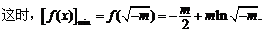
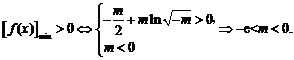 ……………………8分
……………………8分
所以若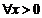 ,
,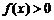 恒成立,则实数m的取值范围是
恒成立,则实数m的取值范围是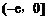 .
.
故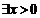 使
使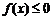 成立,实数m的取值范围
成立,实数m的取值范围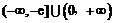 .……………… 10分
.……………… 10分
(3)因为对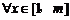 ,
, 所以
所以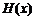 在
在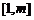 内单调递减.
内单调递减.
于是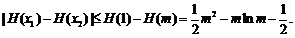
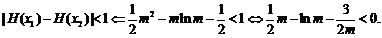 ………………… 12分
………………… 12分
记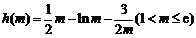 ,
,
则
所以函数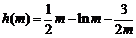 在
在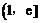 是单调增函数, ………………… 14分
是单调增函数, ………………… 14分
所以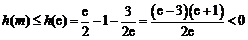 ,故命题成立. ………………… 16分
,故命题成立. ………………… 16分
附加题部分
19.(本小题满分16分)已知椭圆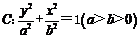 的离心率为
的离心率为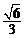 ,过右顶点A的直线l与椭圆C相交于A、B两点,且
,过右顶点A的直线l与椭圆C相交于A、B两点,且 .
.
(1)求椭圆C和直线l的方程;
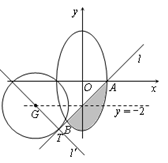
(2)记曲线C在直线l下方的部分与线段AB所围成的平面区域(含边界)为D.若
曲线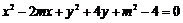 与D有公共点,试求实数m的最小值.
与D有公共点,试求实数m的最小值.
[解](1)由离心率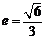 ,得
,得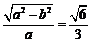 ,即
,即 . ① ………………2分
. ① ………………2分
 又点
又点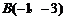 在椭圆
在椭圆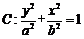 上,即
上,即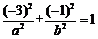 . ② ………………4分
. ② ………………4分
解 ①②得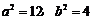 ,
,
故所求椭圆方程为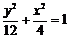 . …………………6分
. …………………6分
由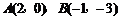 得直线l的方程为
得直线l的方程为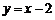 . ………8分
. ………8分
(2)曲线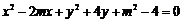 ,
,
即圆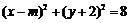 ,其圆心坐标为
,其圆心坐标为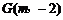 ,半径
,半径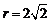 ,表示圆心在直线
,表示圆心在直线
 上,半径为
上,半径为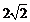 的动圆. ………………… 10分
的动圆. ………………… 10分
由于要求实数m的最小值,由图可知,只须考虑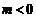 的情形.
的情形.
设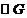 与直线l相切于点T,则由
与直线l相切于点T,则由 ,得
,得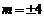 ,………………… 12分
,………………… 12分
当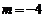 时,过点
时,过点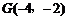 与直线l垂直的直线
与直线l垂直的直线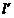 的方程为
的方程为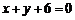 ,
,
解方程组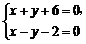 得
得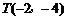 . ………………… 14分
. ………………… 14分
因为区域D内的点的横坐标的最小值与最大值分别为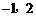 ,
,
所以切点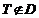 ,由图可知当
,由图可知当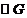 过点B时,m取得最小值,即
过点B时,m取得最小值,即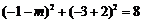 ,
,
解得 . ………………… 16分
. ………………… 16分
(说明:若不说理由,直接由圆过点B时,求得m的最小值,扣4分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com