
3.等比数列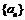 中:
中:
(1)等比数列的符号特征(全正或全负或一正一负),等比数列的首项、公比与等比数列的单调性.
(1)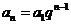
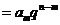 ;
; 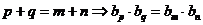 .
.
(3) 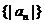 、
、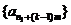 、
、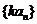 成等比数列;
成等比数列;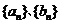 成等比数列
成等比数列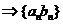 成等比数列.
成等比数列.
(4)两等比数列对应项积(商)组成的新数列仍成等比数列.
(5)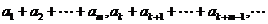 成等比数列.
成等比数列.
(6)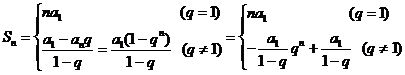 .
.
特别: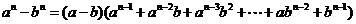 .
.
(7)  .
.
(8)“首大于1”的正值递减等比数列中,前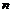 项积的最大值是所有大于或等于1的项的积;“首小于1”的正值递增等比数列中,前
项积的最大值是所有大于或等于1的项的积;“首小于1”的正值递增等比数列中,前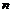 项积的最小值是所有小于或等于1的项的积;
项积的最小值是所有小于或等于1的项的积;
(9)有限等比数列中,奇数项和与偶数项和的存在必然联系,由数列的总项数是偶数还是奇数决定.若总项数为偶数,则“偶数项和”=“奇数项和”与“公比”的积;若总项数为奇数,则“奇数项和”=“首项”加上“公比”与“偶数项和”积的和.
(10)并非任何两数总有等比中项. 仅当实数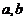 同号时,实数
同号时,实数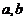 存在等比中项.对同号两实数
存在等比中项.对同号两实数 的等比中项不仅存在,而且有一对
的等比中项不仅存在,而且有一对 .也就是说,两实数要么没有等比中项(非同号时),如果有,必有一对(同号时).在遇到三数或四数成等差数列时,常优先考虑选用“中项关系”转化求解.
.也就是说,两实数要么没有等比中项(非同号时),如果有,必有一对(同号时).在遇到三数或四数成等差数列时,常优先考虑选用“中项关系”转化求解.
(11)判定数列是否是等比数列的方法主要有:定义法、中项法、通项法、和式法(也就是说数列是等比数列的充要条件主要有这四种形式).
注意: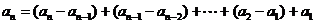 ;
;
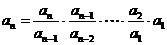 .
.
2.等差数列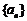 中:
中:
(1)等差数列公差的取值与等差数列的单调性.
(2)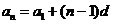
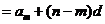 ;
;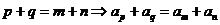 .
.
(3)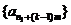 、
、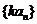 也成等差数列. (4)两等差数列对应项和(差)组成的新数列仍成等差数列.
也成等差数列. (4)两等差数列对应项和(差)组成的新数列仍成等差数列.
(5)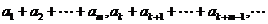 仍成等差数列.
仍成等差数列.
(6)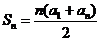 ,
,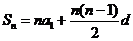 ,
,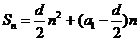 ,
,
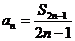 ,
, .
.
(7)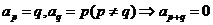 ;
;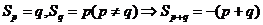 ;
;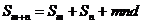 .
.
(8)“首正”的递减等差数列中,前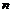 项和的最大值是所有非负项之和;
项和的最大值是所有非负项之和;
“首负”的递增等差数列中,前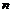 项和的最小值是所有非正项之和;
项和的最小值是所有非正项之和;
(9)有限等差数列中,奇数项和与偶数项和的存在必然联系,由数列的总项数是偶数还是奇数决定.若总项数为偶数,则“偶数项和”-“奇数项和”=总项数的一半与其公差的积;若总项数为奇数,则“奇数项和”-“偶数项和”=此数列的中项.
(10)两数的等差中项惟一存在.在遇到三数或四数成等差数列时,常考虑选用“中项关系”转化求解.
(11)判定数列是否是等差数列的主要方法有:定义法、中项法、通项法、和式法、图像法(也就是说数列是等差数列的充要条件主要有这五种形式).
5.图像变换
(1)函数图像的平移和伸缩变换应注意哪些问题?
函数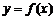 的图像按向量
的图像按向量 平移后,得函数
平移后,得函数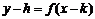 的图像.
的图像.
(2)函数图像的平移、伸缩变换中,图像的特殊点、特殊线也作相应的变换.
(3)图像变换应重视将所研究函数与常见函数(正比例函数、反比例函数、一次函数、二次函数、对数函数、指数函数、三角函数、“鱼钩函数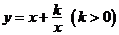 ”及函数
”及函数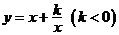 等)相互转化.
等)相互转化.
注意:①形如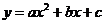 的函数,不一定是二次函数.
的函数,不一定是二次函数.
②应特别重视“二次三项式”、“二次方程”、“二次函数”、“二次曲线”之间的特别联系.
③形如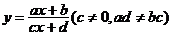 的图像是等轴双曲线,双曲线两渐近线分别直线
的图像是等轴双曲线,双曲线两渐近线分别直线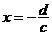 (由分母为零确定)、直线
(由分母为零确定)、直线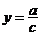 (由分子、分母中
(由分子、分母中 的系数确定),双曲线的中心是点
的系数确定),双曲线的中心是点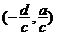 .L
.L
4.对称性与周期性(以下结论要消化吸收,不可强记)
(1)函数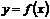 与函数
与函数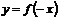 的图像关于直线
的图像关于直线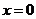 (
( 轴)对称.
轴)对称.
推广一:如果函数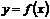 对于一切
对于一切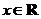 ,都有
,都有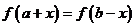 成立,那么
成立,那么 的图像关于直线
的图像关于直线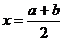 (由“
(由“ 和的一半
和的一半 确定”)对称.
确定”)对称.
推广二:函数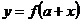 ,
,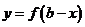 的图像关于直线
的图像关于直线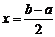 (由
(由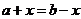 确定)对称.
确定)对称.
(2)函数 与函数
与函数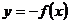 的图像关于直线
的图像关于直线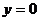 (
( 轴)对称.
轴)对称.
推广:函数 与函数
与函数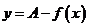 的图像关于直线
的图像关于直线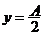 对称(由“
对称(由“ 和的一半
和的一半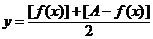 确定”).
确定”).
(3)函数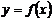 与函数
与函数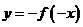 的图像关于坐标原点中心对称.
的图像关于坐标原点中心对称.
推广:函数 与函数
与函数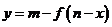 的图像关于点
的图像关于点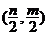 中心对称.
中心对称.
(4)函数 与函数
与函数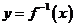 的图像关于直线
的图像关于直线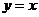 对称.
对称.
推广:曲线 关于直线
关于直线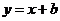 的对称曲线是
的对称曲线是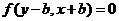 ;
;
曲线 关于直线
关于直线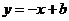 的对称曲线是
的对称曲线是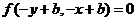 .
.
(5)曲线 绕原点逆时针旋转
绕原点逆时针旋转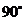 ,所得曲线是
,所得曲线是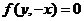 (逆时针横变再交换).
(逆时针横变再交换).
特别: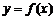 绕原点逆时针旋转
绕原点逆时针旋转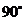 ,得
,得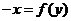 ,若
,若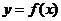 有反函数
有反函数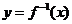 ,则得
,则得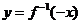 .
.
曲线 绕原点顺时针旋转
绕原点顺时针旋转 ,所得曲线是
,所得曲线是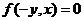 (顺时针纵变再交换).
(顺时针纵变再交换).
特别: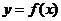 绕原点顺时针旋转
绕原点顺时针旋转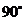 ,得
,得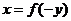 ,若
,若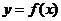 有反函数
有反函数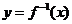 ,则得
,则得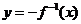 .
.
(6)类比“三角函数图像”得:
若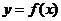 图像有两条对称轴
图像有两条对称轴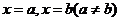 ,则
,则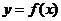 必是周期函数,且一周期为
必是周期函数,且一周期为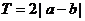 .
.
若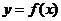 图像有两个对称中心
图像有两个对称中心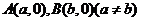 ,则
,则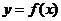 是周期函数,且一周期为
是周期函数,且一周期为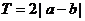 .
.
如果函数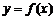 的图像有下一个对称中心
的图像有下一个对称中心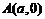 和一条对称轴
和一条对称轴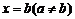 ,则函数
,则函数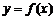 必是周期函数,且一周期为
必是周期函数,且一周期为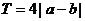 .
.
如果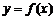 是R上的周期函数,且一个周期为
是R上的周期函数,且一个周期为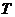 ,那么
,那么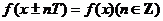 .
.
特别:若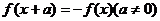 恒成立,则
恒成立,则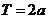 .
.
若 恒成立,则
恒成立,则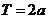 .若
.若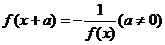 恒成立,则
恒成立,则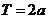 .
.
如果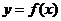 是周期函数,那么
是周期函数,那么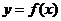 的定义域“无界”.
的定义域“无界”.
3.单调性和奇偶性
(1)奇函数在关于原点对称的区间上若有单调性,则其单调性完全相同.
偶函数在关于原点对称的区间上若有单调性,则其单调性恰恰相反.
单调函数的反函数和原函数有相同的性;如果奇函数有反函数,那么其反函数一定还是奇函数.
注意:(1)确定函数的奇偶性,务必先判定函数定义域是否关于原点对称L.确定函数奇偶性的常用方法有:定义法、图像法等等.
对于偶函数而言有: .
.
(2)若奇函数定义域中有0,则必有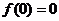 .即
.即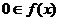 的定义域时,
的定义域时,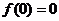 是
是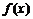 为奇函数的必要非充分条件.
为奇函数的必要非充分条件.
(3)确定函数的单调性或单调区间,在解答题中常用:定义法(取值、作差、鉴定)、导数法;在选择、填空题中还有:数形结合法(图像法)、特殊值法等等.
(4)函数单调是函数有反函数的一个充分非必要条件.
(5)定义在关于原点对称区间上的任意一个函数,都可表示成“一个奇函数与一个偶函数的和(或差)”.
(6)函数单调是函数有反函数的充分非必要条件,奇函数可能反函数,但偶函数只有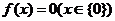 有反函数;既奇又偶函数有无穷多个(
有反函数;既奇又偶函数有无穷多个(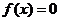 ,定义域是关于原点对称的任意一个数集).
,定义域是关于原点对称的任意一个数集).
(7)复合函数的单调性特点是:“同性得增,增必同性;异性得减,减必异性”.
复合函数的奇偶性特点是:“内偶则偶,内奇同外”.
复合函数要考虑定义域的变化。(即复合有意义)
2.(1)映射是“‘全部射出’加‘一箭一雕’”;映射中第一个集合 中的元素必有像,但第二个集合
中的元素必有像,但第二个集合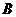 中的元素不一定有原像(
中的元素不一定有原像( 中元素的像有且仅有下一个,但
中元素的像有且仅有下一个,但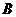 中元素的原像可能没有,也可任意个);函数是“非空数集上的映射”,其中“值域是映射中像集
中元素的原像可能没有,也可任意个);函数是“非空数集上的映射”,其中“值域是映射中像集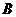 的子集”.
的子集”.
(2)函数图像与 轴垂线至多一个公共点,但与
轴垂线至多一个公共点,但与 轴垂线的公共点可能没有,也可任意个.
轴垂线的公共点可能没有,也可任意个.
(3)函数图像一定是坐标系中的曲线,但坐标系中的曲线不一定能成为函数图像.
(4)原函数与反函数有两个“交叉关系”:自变量与因变量、定义域与值域.求一个函数的反函数,分三步:逆解、交换、定域(确定原函数的值域,并作为反函数的定义域).
注意:①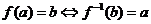 ,
,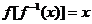 ,
,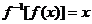 ,
,
但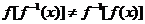 .
.
②L函数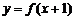 的反函数是
的反函数是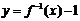 ,而不是
,而不是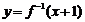 .
.
8.充要条件
7.四种命题中“‘逆’者‘交换’也”、“‘否’者‘否定’也”.
原命题等价于逆否命题,但原命题与逆命题、否命题都不等价.反证法分为三步:假设、推矛、得果.
注意:命题的否定是“命题的非命题,也就是‘条件不变,仅否定结论’所得命题”,但否命题是“既否定原命题的条件作为条件,又否定原命题的结论作为结论的所得命题” L.
6.“或命题”的真假特点是“一真即真,要假全假”;“且命题”的真假特点是“一假即假,要真全真”;“非命题”的真假特点是“一真一假”.
5.判断命题的真假
关键是“抓住关联字词”;注意:“不‘或’即‘且’,不‘且’即‘或’”.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com