
4.线性规划中几个概念:约束条件、可行解、可行域、目标函数、最优解.
3.相交两直线的夹角和两直线间的到角是两个不同的概念:夹角特指相交两直线所成的较小角,范围是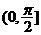 ,而其到角是带有方向的角,范围是
,而其到角是带有方向的角,范围是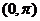 .相应的公式是:夹角公式
.相应的公式是:夹角公式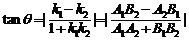 ,直线
,直线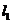 到
到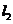 角公式
角公式 .注:点到直线的距离公式
.注:点到直线的距离公式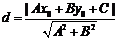 .
.
特别: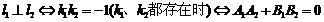 ;
;
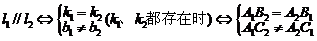 ;
;
 .
.
2.知直线纵截距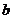 ,常设其方程为
,常设其方程为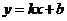 或
或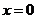 ;知直线横截距
;知直线横截距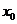 ,常设其方程为
,常设其方程为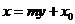 (直线斜率k存在时,
(直线斜率k存在时,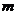 为k的倒数)或
为k的倒数)或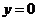 .知直线过点
.知直线过点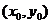 ,常设其方程为
,常设其方程为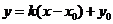 或
或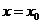 .
.
注意:(1)直线方程的几种形式:点斜式、斜截式、两点式、截矩式、一般式、向量式.以及各种形式的局限性.(如点斜式不适用于斜率不存在的直线,还有截矩式呢?)
与直线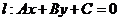 平行的直线可表示为
平行的直线可表示为 ;
;
与直线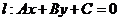 垂直的直线可表示为
垂直的直线可表示为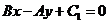 ;
;
过点 与直线
与直线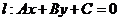 平行的直线可表示为:
平行的直线可表示为:
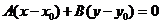 ;
;
过点 与直线
与直线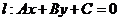 垂直的直线可表示为:
垂直的直线可表示为:
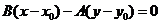 .
.
(2)直线在坐标轴上的截距可正、可负、也可为0.直线两截距相等 直线的斜率为-1或直线过原点;直线两截距互为相反数
直线的斜率为-1或直线过原点;直线两截距互为相反数 直线的斜率为1或直线过原点;直线两截距绝对值相等
直线的斜率为1或直线过原点;直线两截距绝对值相等 直线的斜率为
直线的斜率为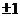 或直线过原点.
或直线过原点.
(3)在解析几何中,研究两条直线的位置关系时,有可能这两条直线重合,而在立体几何中一般提到的两条直线可以理解为它们不重合.
1.直线倾斜角与斜率的存在性及其取值范围;直线方向向量的意义(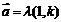 或
或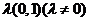 )及其直线方程的向量式(
)及其直线方程的向量式(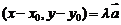 (
(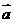 为直线的方向向量)).应用直线方程的点斜式、斜截式设直线方程时,一般可设直线的斜率为k,但你是否注意到直线垂直于x轴时,即斜率k不存在的情况?
为直线的方向向量)).应用直线方程的点斜式、斜截式设直线方程时,一般可设直线的斜率为k,但你是否注意到直线垂直于x轴时,即斜率k不存在的情况?
5.含绝对值不等式的性质:
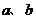 同号或有
同号或有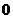

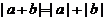

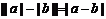 ;
;
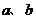 异号或有
异号或有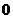

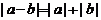

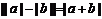 .
.
注意:不等式恒成立问题的常规处理方式?(常应用方程函数思想和“分离变量法”转化为最值问题).
4.比较大小的方法和证明不等式的方法主要有:差比较法、商比较法、函数性质法、综合法、分析法和放缩法(注意:对“整式、分式、绝对值不等式”的放缩途径, “配方、函数单调性等”对放缩的影响).
3.常用不等式有: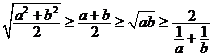 (根据目标不等式左右的运算结构选用) a、b、c
(根据目标不等式左右的运算结构选用) a、b、c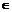 R,
R, (当且仅当
(当且仅当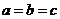 时,取等号)
时,取等号)
2. 利用重要不等式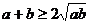 以及变式
以及变式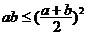 等求函数的最值时,务必注意a,b
等求函数的最值时,务必注意a,b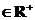 (或a ,b非负),且“等号成立”时的条件是积ab或和a+b其中之一应是定值(一正二定三等四同时).
(或a ,b非负),且“等号成立”时的条件是积ab或和a+b其中之一应是定值(一正二定三等四同时).
1.(1)解不等式是求不等式的解集,最后务必有集合的形式表示;不等式解集的端点值往往是不等式对应方程的根或不等式有意义范围的端点值.
(2)解分式不等式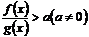 的一般解题思路是什么?(移项通分,分子分母分解因式,x的系数变为正值,标根及奇穿过偶弹回);
的一般解题思路是什么?(移项通分,分子分母分解因式,x的系数变为正值,标根及奇穿过偶弹回);
(3)含有两个绝对值的不等式如何去绝对值?(一般是根据定义分类讨论、平方转化或换元转化);
(4)解含参不等式常分类等价转化,必要时需分类讨论.注意:按参数讨论,最后按参数取值分别说明其解集,但若按未知数讨论,最后应求并集.
8.平移与定比分点
(1)线段的定比分点坐标公式
设P(x,y)、P1(x1,y1),P2(x2,y2),且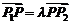 ,则.
,则.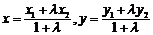 ,
,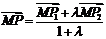 .
.
特别:分点的位置与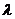 的对应关系.
的对应关系.
中点坐标公式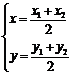 ,
,
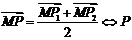 为
为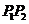 的中点.
的中点.
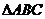 中,
中,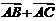 过
过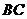 边中点;
边中点;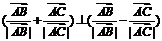 ;
;
 .
.
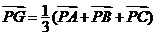

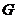 为
为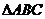 的重心;
的重心;
特别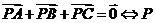 为
为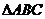 的重心.
的重心.
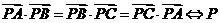 为
为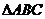 的垂心;
的垂心;
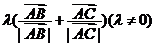 所在直线过
所在直线过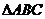 的内心(是
的内心(是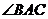 的角平分线所在直线);
的角平分线所在直线);
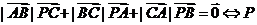
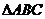 的内心.
的内心.
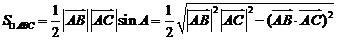 .
.
(2)平移公式: 如果点P(x,y)按向量a=(h,k)平移至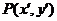 ,则
,则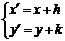 .
.
曲线 按向量a=(h,k)平移得曲线
按向量a=(h,k)平移得曲线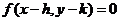 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com