
6.注意应用函数的导数,考察函数单调性、最值(极值),研究函数的性态,数形结合解决方程不等式等相关问题.
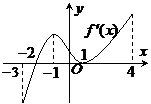
5.微积分的创始人是牛顿、莱布尼兹.
4.应用导数求曲线的切线方程,要以“切点坐标”为桥梁,注意题目中是“处L”还是“过L”,对“二次抛物线”过抛物线上一点的切线 抛物线上该点处的切线,但对“三次曲线”过其上一点的切线包含两条,其中一条是该点处的切线,另一条是与曲线相交于该点.
抛物线上该点处的切线,但对“三次曲线”过其上一点的切线包含两条,其中一条是该点处的切线,另一条是与曲线相交于该点.
3.导数与极值、导数与最值:
(1)函数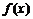 在
在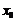 处有
处有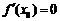 且“左正右负”
且“左正右负”
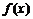 在
在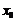 处取极大值;
处取极大值;
函数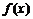 在
在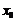 处有
处有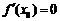 且“左负右正”
且“左负右正”
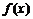 在
在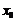 处取极小值.
处取极小值.
注意:①在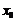 处有
处有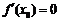 是函数
是函数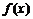 在
在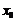 处取极值的必要非充分条件.
处取极值的必要非充分条件.
②求函数极值的方法:先找定义域,再求导,找出定义域的分界点,列表求出极值. 特别是给出函数极大(小)值的条件,一定要既考虑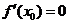 ,又要考虑验“左正右负”(“左负右正”)的转化,否则条件没有用完,这一点一定要切记.
,又要考虑验“左正右负”(“左负右正”)的转化,否则条件没有用完,这一点一定要切记.
③单调性与最值(极值)的研究要注意列表!
(2)函数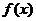 在一闭区间上的最大值是此函数在此区间上的极大值与其端点值中的“最大值”;
在一闭区间上的最大值是此函数在此区间上的极大值与其端点值中的“最大值”;
函数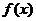 在一闭区间上的最小值是此函数在此区间上的极小值与其端点值中的“最小值”;
在一闭区间上的最小值是此函数在此区间上的极小值与其端点值中的“最小值”;
注意:利用导数求最值的步骤:先找定义域 再求出导数为0及导数不存在的的点,然后比较定义域的端点值和导数为0的点对应函数值的大小,其中最大的就是最大值,最小就为最小值.
2.多项式函数的导数与函数的单调性:
在一个区间上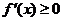 (个别点取等号)
(个别点取等号)
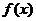 在此区间上为增函数.
在此区间上为增函数.
在一个区间上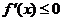 (个别点取等号)
(个别点取等号)
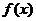 在此区间上为减函数.
在此区间上为减函数.
1.导数的意义:曲线在该点处的切线的斜率(几何意义)、瞬时速度、边际成本(成本为因变量、产量为自变量的函数的导数).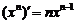 ,
,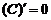 (C为常数),
(C为常数),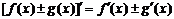 ,
,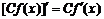 .
.
3.用样本的算术平均数作为对总体期望值的估计;用样本方差的大小估计总体数据波动性的好差(方差大波动差).公式如下:
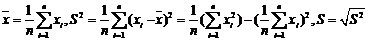 (标准方差)
(标准方差)
样本数据做如下变换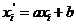 ,则
,则 ,
,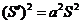 .
.
总体估计还要掌握:(1)一“表”(频率分布表)一“图”(频率分布直方图).
注意:直方图的纵轴(小矩形的高)一般是频率除以组距的商L (而不是频率),横轴一般是数据的大小,小矩形的面积表示频率L.
2.总体分布的估计就是用总体中样本的频率作为总体的概率.
1.抽样方法:(1)简单随机抽样(抽签法、随机样数表法)常常用于总体个数较少时,它的主要特征是从总体中逐个抽取.(2)分层抽样,主要特征分层按比例抽样,主要使用于总体中有明显差异.共同点:每个个体被抽到的概率都相等(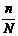 )
)
5.概率的计算公式:
(1)等可能事件的概率计算公式: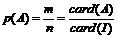 ;
;
(2)互斥事件的概率计算公式:P(A+B)=P(A)+P(B);
(3)对立事件的概率计算公式是:P(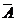 )=1-P(A);
)=1-P(A);
(4)独立事件同时发生的概率计算公式是:P(A•B)=P(A)•P(B);
(5)独立事件重复试验的概率计算公式是:
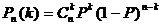 (是二项展开式[(1-P)+P]n的第(k+1)项).
(是二项展开式[(1-P)+P]n的第(k+1)项).
注意:探求一个事件发生的概率,常应用等价转化思想和分解(分类或分步)转化思想处理:把所求的事件转化为等可能事件的概率(常常采用排列组合的知识);转化为若干个互斥事件中有一个发生的概率;利用对立事件的概率,转化为相互独立事件同时发生的概率;看作某一事件在n次实验中恰有k次发生的概率,但要注意公式的使用条件. 事件互斥是事件独立的必要非充分条件,反之,事件对立是事件互斥的充分非必要条件.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com