4.甲、乙两人下棋，甲获胜的概率是40%，甲不输的概率为90%，则甲、乙二人下成和棋的概率为

A.60%　　　　　　　 B.30%　　　　　　　 C.10%　　　　　　　 D.50%

3.(2004江苏)将一颗质地均匀的骰子(它是一种各面上分别标有点数1、2、3、4、3.6的正方体玩具)先后抛掷3次，至少出现一次6点向上的概率是　　　　 (　 )

A.　　　　　　　 B.　　　　　　 　C.　　　　　　　 D.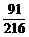

2．(2005湖北)以平行六面体ABCD-A′B′C′D′的任意三个顶点为顶点作三角形，从中随机取出两个三角形，则这两个三角形不共面的概率p为(　 )

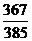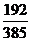A．　　　　　　　　　 B．　　　　　　　　　 C．　　　　　　　　　 D．

1．(2005山东)10张奖券中只有3张有奖，5个人购买，每人一张，至少有1人中奖的概率是　　　　 (　 )

A．　　　　　　　　　　 B．　　　　　　　　　　 C． 　　　　　　　　　　 D．

5．互斥事件概率的计算反映了分类讨论的思想；而则体现了“正难则反”的策略，在解题中要注意灵活运用。

4.对于互斥事件理解：

(1)互斥事件是一次试验中所发生的事件，这些事件不能同时出现。

从集合角度来看，两个事件互斥A、B所含结果组成的集合的交集是空集。

(2)对立事件是互斥事件的特殊情况，是指在一次试验中的两个事件有且仅有一个发生， A∩=， A∪=U(全集)。

(3)事件的和的意义:当A、B为互斥事件时， A、B中至少有一个发生的事件叫做A、B的和事件，记作A+B，易知：

P(A+B)=P(A)+P(B)- P(A·B)

其中P(A·B)表示A、B同时发生的概率。

3．对立事件的概念:如果事件A、B互斥，且必有一个发生，则称A、B为对立事件，A的对立事件记为。

显然 P(A+)=P(A)+ P()＝1也即。

2.互斥事件有一个发生的概率：

如果事件A、B互斥，则事件A、B有一个发生的概率 P(A+B)=P(A)+ P(B) 。

事件A、B同时发生的概率P(A•B)=0)。

一般地，如果事件A₁、A₂、……A_n彼此互斥 那么A₁、A₂、……A_n中有一个发生的概率P(A₁+A₂+……+A_n))=P(A₁)+ P(A₂)+……+ P(A_n).

1．互斥事件的概念:不可能同时发生的个事件叫做互斥事件。

一般地：如果事件A₁、A₂、……A_n中的任何两个都是互斥的，那么就说事件A₁、A₂、……A_n彼此互斥。

了解互斥事件的意义，会用互斥事件的概率加法公式计算一些事件的概率。