
11、(四川省成都市新都一中高2008级12月月考)通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散.分析结果和实验表明,用f(x)表示学生掌握和接受概念的能力(f(x)的值越大,表示接受能力越强),x表示提出和讲授概念的时间(单位:分),可以有以下公式: f(x)= (1)开讲多少分钟后,学生的接受能力最强?能维持多少分钟? (2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些? (3)一个数学难题,需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题? 解:(1)当0<x≤10时,f(x)=-0.1x2+2.6x+43=-0.1(x-13)2+59.9 故f(x)在0<x≤10时递增,最大值为f(10)=-0.1(10-13)2+59.9=59 当10<x≤16时,f(x)≡59 当x>16时,f(x)为减函数,且f(x)<59 因此,开讲10分钟后,学生达到最强接受能力(为59),能维持6分钟时间.…………5分 (2)f(5)=-0.1(5-13)2+59.9=53.5 f(20)=-3×20+107=47<53.5 故开讲5分钟时学生的接受能力比开讲20分钟时要强一些.……………………………8分 (3)当0<x≤10时,令f(x)=55,解得x=6或20(舍) 当x>16时,令f(x)=55,解得x=17 因此学生达到(含超过)55的接受能力的时间为17-6=11<13(分) 老师来不及在学生一直达到所需接受能力的状态下讲授完这个难题.
10、(四川省成都市一诊)已知函数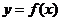 是定义域为R的偶函数,其图像均在x轴的上方,对任意的
是定义域为R的偶函数,其图像均在x轴的上方,对任意的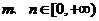 ,都有
,都有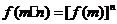 ,且
,且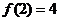 ,又当
,又当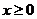 时,其导函数
时,其导函数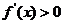 恒成立。
恒成立。
(Ⅰ)求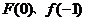 的值;
的值;
(Ⅱ)解关于x的不等式: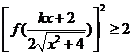 ,其中
,其中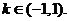
解:(1)由f(m·n)=[f(m)]n得:f(0)=f(0×0)=[f(0)]0
∵函数f(x)的图象均在x轴的上方,∴f(0)>0,∴f(0)=1 ……3分
∵f(2)=f(1×2)=[f(1)]2=4,又f(x)>0
∴f(1)=2,f(-1)=f(1)=2 ……3分
(2)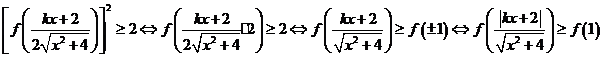
又当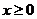 时,其导函数
时,其导函数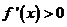 恒成立,∴
恒成立,∴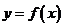 在区间
在区间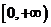 上为单调递增函数
上为单调递增函数
∴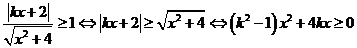
①当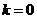 时,
时,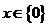 ;
;
②当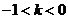 时,
时,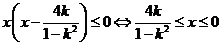 ,∴
,∴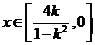 ;
;
③当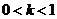 时,
时,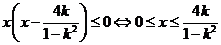 ,∴
,∴
综上所述:当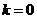 时,
时,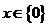 ;当
;当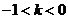 时,
时,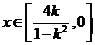 ;
;
当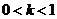 时,
时, 。
。
9、(四川省成都市新都一中高2008级一诊适应性测试)某机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利(盈利额为正值)
(3)使用若干年后,对机床的处理方案有两种:(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由.
解:(1)依题得: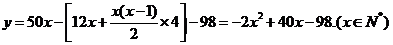
……3分
(2)解不等式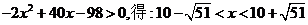
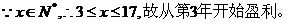 ……6分
……6分
(3)(Ⅰ)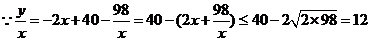
当且仅当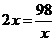 时,即x=7时等号成立.
时,即x=7时等号成立.
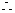 到2008年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.……10分
到2008年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.……10分
(Ⅱ)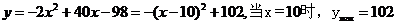
故到2011年,盈利额达到最大值,工厂获利102+12=114万元 ……11分
盈利额达到的最大值相同,而方案Ⅰ所用的时间较短,故方案Ⅰ比较合理.
8、(陕西长安二中2008届高三第一学期第二次月考)已知二次函数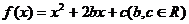 满足
满足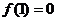 ,且关于
,且关于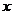 的方程
的方程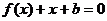 的两实数根分别在区间(-3,-2),(0,1)内。
的两实数根分别在区间(-3,-2),(0,1)内。
(1)求实数 的取值范围;
的取值范围;
(2)若函数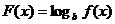 在区间(-1-
在区间(-1-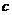 ,1-
,1-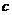 )上具有单调性,求实数C的取值范围
)上具有单调性,求实数C的取值范围
解:(1)由题意知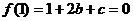 ,∴
,∴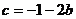
记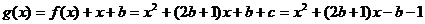
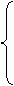 则
则 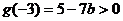
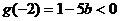
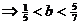
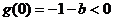
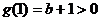
即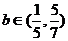
(2)令u=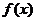 。∵
。∵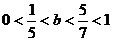 ∴
∴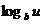 在(0,+∞)是减函数
在(0,+∞)是减函数
而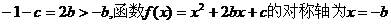
∴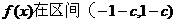 上为增函数,
上为增函数,
从而 上为减函数。
上为减函数。
且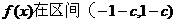 上恒有
上恒有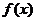 >0 ,只需
>0 ,只需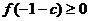 ,
,
且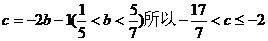
7、(陕西长安二中2008届高三第一学期第二次月考)定义在R上的函数y=f(x),f(0)≠0,当x>0时,f(x)>1,且对任意的a、b∈R,有f(a+b)=f(a)f(b),
(1)求证:f(0)=1;(2)求证:对任意的x∈R,恒有f(x)>0;
(3)证明:f(x)是R上的增函数;(4)若f(x)·f(2x-x2)>1,求x的取值范围。
解:(1)令a=b=0,则f(0)=[f(0)]2∵ f(0)≠0 ∴ f(0)=1
(2)令a=x,b=-x则 f(0)=f(x)f(-x) ∴ 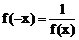
由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0
∴ 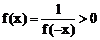 又x=0时,f(0)=1>0
又x=0时,f(0)=1>0
∴ 对任意x∈R,f(x)>0
(3)任取x2>x1,则f(x2)>0,f(x1)>0,x2-x1>0
∴

∴ f(x2)>f(x1) ∴ f(x)在R上是增函数
(4)f(x)·f(2x-x2)=f[x+(2x-x2)]=f(-x2+3x) 又1=f(0),f(x)在R上递增
∴ 由f(3x-x2)>f(0)得:x-x2>0 ∴ 0<x<3
6、(陕西长安二中2008届高三第一学期第二次月考)为了保护环境,实现城市绿化,某房地产公司要在拆迁地长方形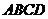 上规划出一块长方形地面建造公园,公园一边落在CD上,但不得越过文物保护区
上规划出一块长方形地面建造公园,公园一边落在CD上,但不得越过文物保护区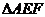 的EF.问如何设计才能使公园占地面积最大,并求这最大面积.( 其中AB=200m,BC=160m,AE=60m,AF=40m.)
的EF.问如何设计才能使公园占地面积最大,并求这最大面积.( 其中AB=200m,BC=160m,AE=60m,AF=40m.)
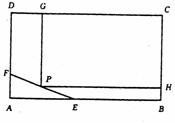 解:设CG=X,矩形CGPH面积为Y,
解:设CG=X,矩形CGPH面积为Y,
如图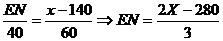
∴HC=160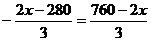
∴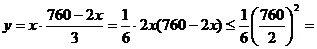
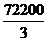
当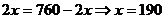 (m)即CG长为190m时,最大面积为
(m)即CG长为190m时,最大面积为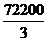 (m2)
(m2)
5、(陕西长安二中2008届高三第一学期第二次月考)已知函数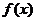 =
=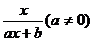 的图像过点(-4,4),且关于直线
的图像过点(-4,4),且关于直线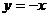 成轴对称图形,试确定
成轴对称图形,试确定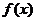 的解析式.
的解析式.
解:由题意得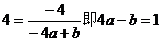 ………①
………①
又 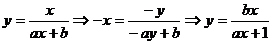
∴b=1代入①得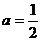 ,∴
,∴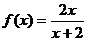
4、(陕西长安二中2008届高三第一学期第二次月考)已知函数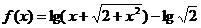
(1)判断函数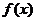 的奇偶性。 (2)判断函数
的奇偶性。 (2)判断函数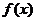 的单调性。
的单调性。
解:(1)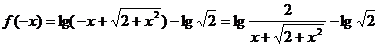
=
∴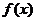 为奇函数
为奇函数
(2)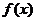 是R上的增函数,(证明略)
是R上的增函数,(证明略)
3、(陕西长安二中2008届高三第一学期第二次月考)求函数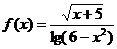 的定义域:
的定义域:
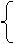 解:由题意得
解:由题意得
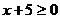
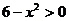
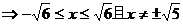
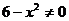
2、(江苏省启东中学高三综合测试二)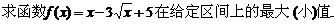
解:设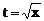 ,则
,则 f(t)的顶点横坐标为
f(t)的顶点横坐标为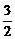 ,属于
,属于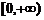 ,故f(t)在
,故f(t)在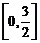 上是减函数,在
上是减函数,在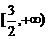 为增函数,所以最小值在
为增函数,所以最小值在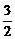 达到,为
达到,为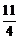 ,当
,当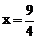 时达到最小值
时达到最小值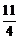 ,该函数没有最大值
,该函数没有最大值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com