
21、(广东省2008届六校第二次联考)已知集合 是满足下列性质的函数
是满足下列性质的函数 的全体, 存在非零常数
的全体, 存在非零常数 , 对任意
, 对任意 , 有
, 有 成立.
成立.
(1) 函数 是否属于集合
是否属于集合 ? 说明理由;
? 说明理由;
(2) 设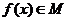 , 且
, 且 , 已知当
, 已知当 时,
时,  ,
求当
,
求当 时,
时,  的解析式.
的解析式.
解: (1) 假设函数 属于集合
属于集合 , 则存在非零常数
, 则存在非零常数 , 对任意
, 对任意 , 有
, 有 成立,
成立,
即: 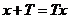 成立. 令
成立. 令 , 则
, 则 , 与题矛盾. 故
, 与题矛盾. 故 .
.
(2) 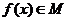 ,
且
,
且 , 则对任意
, 则对任意 , 有
, 有 ,
,
设 , 则
, 则 ,
, 
当 时,
时,  ,
,
故当 时,
时,  .
.
20、(甘肃省兰州一中2008届高三上期期末考试)已知函数 成等差数列.
成等差数列.
(Ⅰ)求 的值;
的值;
(Ⅱ)若a,b,c是两两不相等的正数,且a,b,c成等比数列,试判断 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
解:(Ⅰ)由 成等差数列,得
成等差数列,得 ,即
,即
 ……5分
……5分
(Ⅱ)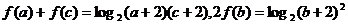 …………7分
…………7分
∵ ………………8分
………………8分
∵ …………10分
…………10分
∴
19、(福建省师大附中2008年高三上期期末考试)设函数 。
。
(1)求 的单调区间;
的单调区间;
(2)是否存在正实数 ,使函数
,使函数 的定义域为
的定义域为 时值域为
时值域为 ?
?
若存在,求 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。

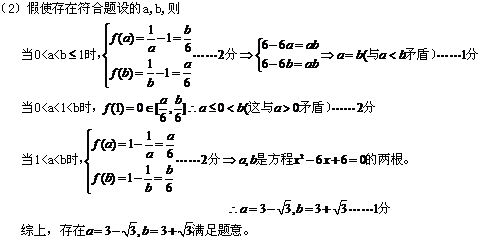
18、(福建省师大附中2008年高三上期期末考试)已知函数 ,
,
(1)讨论函数 的奇偶性,并说明理由。
的奇偶性,并说明理由。
(2)若函数 在
在 上是增函数,求
上是增函数,求 的取值范围。
的取值范围。
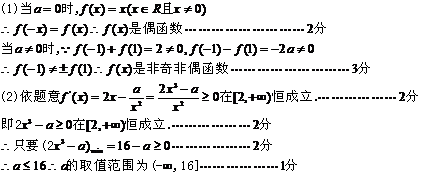
17、(本小题满分12分)已知函数 的定义域为
的定义域为 ,
(1)求M
(2)当
,
(1)求M
(2)当 时,求
时,求
 的最小值.
解 (1)
的最小值.
解 (1)
 (…………4分)
(…………4分)
(2) =
=
又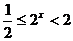 ,
, ,
, (…………………6分)
(…………………6分)
①若 ,即
,即 时,
时, =
=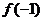 =
= ,(…………8分)
,(…………8分)
②若 ,即
,即
 时,
时,
所以当 即
即 时,
时, =
= (………………11分)
(………………11分)

16、(四川省成都市高2008届毕业班摸底测试)已知向量 的图象按向量m平移后得到函数
的图象按向量m平移后得到函数 的图象。
的图象。
(Ⅰ)求函数 的表达式;
的表达式;
(Ⅱ)若函数 上的最小值为
上的最小值为 的最大值。
的最大值。
解:(Ⅰ)设P(x,y)是函数 图象上的任意一点,它在函数
图象上的任意一点,它在函数 图象上的对应点
图象上的对应点 ,则由平移公式,得
,则由平移公式,得 …………2分
…………2分
∴ 代入函数
代入函数 中,得
中,得
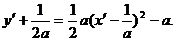 ………………2分
………………2分
∴函数 的表达式为
的表达式为 …………1分
…………1分
(Ⅱ)函数 的对称轴为
的对称轴为
①当 时,函数
时,函数 在[
在[ ]上为增函数,
]上为增函数,
∴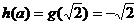 ………………2分
………………2分
②当 时,
时,
∴
当且仅当 时取等号; …………2分
时取等号; …………2分
③当 时,函数
时,函数 在[
在[ ]上为减函数,
]上为减函数,
∴ …………2分
…………2分
综上可知,
∴当 时,函数
时,函数 的最大值为
的最大值为 
15、(山东省博兴二中高三第三次月考)已知函数f(x)的定义域为{x| x ≠ kπ,k ∈ Z},且对于定义域内的任何x、y,有f(x - y) = 成立,且f(a) = 1(a为正常数),当0 < x < 2a时,f(x) > 0.(I)判断f(x)奇偶性;(II)证明f(x)为周期函数;(III)求f (x)在[2a,3a] 上的最小值和最大值.
解:(1)∵定义域{x| x ≠ kπ,k∈Z }关于原点对称,
又f(- x) = f [(a - x) - a]= = = = = = - f (x),对于定义域内的每个x值都成立
∴ f(x)为奇函数------------------------------------------------------------------------------------(4分)
(2)易证:f(x + 4a) = f(x),周期为4a.------------------------------------------(8分)
(3)f(2a)= f(a + a)= f [a -(- a)]= = = 0,
f(3a)= f(2a + a)= f [2a -(- a)]= = = - 1.
先证明f(x)在[2a,3a]上单调递减为此,必须证明x∈(2a,3a)时,f(x) < 0,
设2a < x < 3a,则0 < x - 2a < a,
∴ f(x - 2a)= = - > 0,∴ f(x)< 0---------------------(10分)
设2a < x1 < x2 < 3a,
则0 < x2 - x1 < a,∴ f(x1)< 0 f(x2)< 0 f(x2 - x1)> 0,
∴ f(x1)- f(x2)= > 0,∴ f(x1)> f(x2),
∴ f(x)在[2a,3a]上单调递减--------------------------------------------------(12分)
∴ f(x)在[2a,3a]上的最大值为f(2a = 0,最小值为f(3a)= - 1
14、(北京市十一学校2008届高三数学练习题)对于函数 ,若存在
,若存在 ,使
,使 成立,则称
成立,则称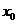 为
为 的不动点.如果函数
的不动点.如果函数 有且仅有两个不动点
有且仅有两个不动点 、
、 ,且
,且 .
.
(Ⅰ)试求函数 的单调区间;
的单调区间;
(Ⅱ)已知各项不为零的数列 满足
满足 ,求证:
,求证: ;
;
(Ⅲ)设 ,
, 为数列
为数列 的前
的前 项和,求证:
项和,求证: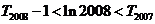 .
.
解:(Ⅰ)设
 ∴
∴ ∴
∴
由
又∵ ∴
∴
∴ …………………… 3分
…………………… 3分
于是
由 得
得 或
或 ; 由
; 由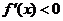 得
得 或
或
故函数 的单调递增区间为
的单调递增区间为 和
和 ,
,
单调减区间为 和
和 ……………………4分
……………………4分
(Ⅱ)由已知可得 , 当
, 当 时,
时,
两式相减得
∴ 或
或
当 时,
时, ,若
,若 ,则
,则 这与
这与 矛盾
矛盾
∴ ∴
∴ ……………………6分
……………………6分
于是,待证不等式即为 .
.
为此,我们考虑证明不等式
令 则
则 ,
,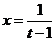
再令 ,
, 由
由 知
知
∴当 时,
时, 单调递增 ∴
单调递增 ∴ 于是
于是
即 ①
①
令 ,
, 由
由 知
知
∴当 时,
时, 单调递增 ∴
单调递增 ∴ 于是
于是
即 ②
②
由①、②可知 ……………………10分
……………………10分
所以, ,即
,即 ……11分
……11分
(Ⅲ)由(Ⅱ)可知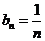 则
则
在 中令
中令 ,并将各式相加得
,并将各式相加得

即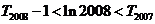
13、(北京市海淀区2008年高三统一练习一)一个函数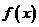 ,如果对任意一个三角形,只要它的三边长
,如果对任意一个三角形,只要它的三边长 都在
都在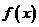 的定义域内,就有
的定义域内,就有 也是某个三角形的三边长,则称
也是某个三角形的三边长,则称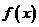 为“保三角形函数”.
为“保三角形函数”.
(I)判断 ,
, ,
, 中,哪些是“保三角形函数”,哪些不是,并说明理由;
中,哪些是“保三角形函数”,哪些不是,并说明理由;
(II)如果 是定义在
是定义在 上的周期函数,且值域为
上的周期函数,且值域为 ,证明
,证明 不是“保三角形函数”;
不是“保三角形函数”;
(III)若函数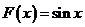 ,
,
 是“保三角形函数”,求
是“保三角形函数”,求 的最大值.
的最大值.
(可以利用公式 )
)
解:(I) 是“保三角形函数”,
是“保三角形函数”, 不是“保三角形函数”.
1分
不是“保三角形函数”.
1分
任给三角形,设它的三边长分别为 ,则
,则 ,不妨假设
,不妨假设 ,
,
由于 ,所以
,所以 是“保三角形函数”. 3分
是“保三角形函数”. 3分
对于 ,3,3,5可作为一个三角形的三边长,但
,3,3,5可作为一个三角形的三边长,但 ,所以不存在三角形以
,所以不存在三角形以 为三边长,故
为三边长,故 不是“保三角形函数”.
4分
不是“保三角形函数”.
4分
(II)设 为
为 的一个周期,由于其值域为
的一个周期,由于其值域为 ,所以,存在
,所以,存在 ,使得
,使得 ,
,
取正整数 ,可知
,可知 这三个数可作为一个三角形的三边长,但
这三个数可作为一个三角形的三边长,但 ,
, 不能作为任何一个三角形的三边长.故
不能作为任何一个三角形的三边长.故 不是“保三角形函数”.
8分
不是“保三角形函数”.
8分
(III) 的最大值为
的最大值为 .
9分
.
9分
一方面,若 ,下证
,下证 不是“保三角形函数”.
不是“保三角形函数”.
取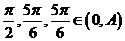 ,显然这三个数可作为一个三角形的三边长,但
,显然这三个数可作为一个三角形的三边长,但
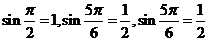 不能作为任何一个三角形的三边长,故
不能作为任何一个三角形的三边长,故 不是“保三角形函数”.
不是“保三角形函数”.
另一方面,以下证明 时,
时, 是“保三角形函数”.
是“保三角形函数”.
对任意三角形的三边 ,若
,若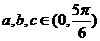 ,则分类讨论如下:
,则分类讨论如下:
(1) ,
,
此时 ,同理,
,同理, ,
,
∴ ,故
,故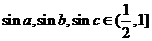 ,
, .
.
同理可证其余两式.
∴ 可作为某个三角形的三边长.
可作为某个三角形的三边长.
(2)
此时,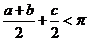 ,可得如下两种情况:
,可得如下两种情况:
 时,由于
时,由于 ,所以,
,所以, .
.
由 在
在 上的单调性可得
上的单调性可得 ;
;
 时,
时, ,
,
同样,由 在
在 上的单调性可得
上的单调性可得 ;
;
总之, .
.
又由 及余弦函数在
及余弦函数在 上单调递减,得
上单调递减,得
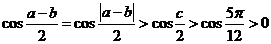 ,
,
∴ .
.
同理可证其余两式,所以 也是某个三角形的三边长.故
也是某个三角形的三边长.故 时,
时, 是“保三角形函数”.
是“保三角形函数”.
综上, 的最大值为
的最大值为 .
.
12、(北京市东城区2008年高三综合练习二)已知函数 满足下列条件:
满足下列条件:
①函数 的定义域为[0,1];
的定义域为[0,1];
②对于任意
 ;
;
③对于满足条件 的任意两个数
的任意两个数
(1)证明:对于任意的 ;
;
(2)证明:于任意的 ;
;
(3)不等式 对于一切x∈[0,1]都成立吗?试说明理由.
对于一切x∈[0,1]都成立吗?试说明理由.
(1)证明:对于任意的

即对于任意的 ……………………………………5分
……………………………………5分
(2)证明:由已知条件可得


所以对于任意的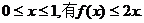 …………………………………………10分
…………………………………………10分
(3)解:取函数
则 显然满足题目中的(1),(2)两个条件,
显然满足题目中的(1),(2)两个条件,
任意取两个数


即不等式
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com