
31、(江苏省南京市2008届高三第一次调研测试)已知函数f (x) =
(1)判断函数f (x)在区间(0, +∞)上的单调性,并加以证明;
(2)如果关于x的方程f (x) = kx2有四个不同的实数解,求实数k的取值范围.
解(1)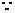
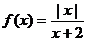 ,
,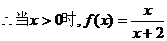 .
.
 …………………………2分
…………………………2分
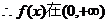 上单调递增函数.……………………4分
上单调递增函数.……………………4分
(2)原方程即: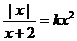
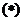
①
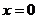 恒为方程
恒为方程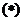 的一个解.……………………5分
的一个解.……………………5分
②当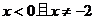 时方程
时方程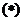 有解,则
有解,则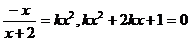
当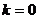 时,方程
时,方程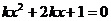 无解;
无解;
当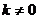 时,
时,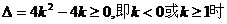 ,方程
,方程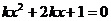 有解.
有解.
设方程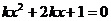 的两个根分别是
的两个根分别是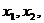 则
则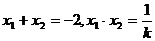 .
.
当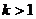 时,方程
时,方程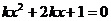 有两个不等的负根;…………………7分
有两个不等的负根;…………………7分
当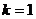 时,方程
时,方程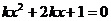 有两个相等的负根;………………9分.
有两个相等的负根;………………9分.
当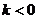 时,方程
时,方程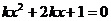 有一个负根………………………11分
有一个负根………………………11分
③当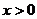 时,方程
时,方程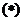 有解,则
有解,则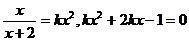
当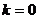 时,方程
时,方程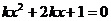 无解;
无解;
当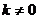 时,
时,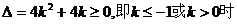 ,方程
,方程 有解.
有解.
设方程 的两个根分别是
的两个根分别是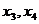
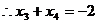 ,
,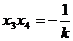
 当
当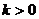 时,方程
时,方程 有一个正根,
有一个正根,
当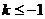 时,方程
时,方程 没有正根.……………………13分.
没有正根.……………………13分.
综上可得,当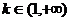 时,方程
时,方程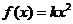 有四个不同的实数解.……16分.
有四个不同的实数解.……16分.
30、(江苏省南京市2008届高三第一次调研测试)经市场调查,某种商品在过去50天的销售和价格均为销售时间t(天)的函数,且销售量近似地满足f (t) = – 2t + 200(1 ≤ t ≤ 50 , t ∈ N ),前30天价格为g (t) = t + 30 (1 ≤ t ≤ 30 , t ∈ N ),后20天价格为g (t) = 45 (31 ≤ t ≤ 50 , t ∈ N ).
(1)写出该种商品的日销售S与时间t的函数关系;
(2)求日销售S的最大值.
解:(1)根据题意得: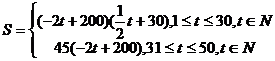
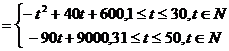 ………………7分
………………7分
(2)①当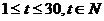 时,
时,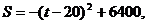
当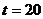 时,
时,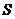 的最大值为
的最大值为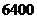 ………………………………10分
………………………………10分
②当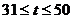 ,
,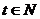 时,
时,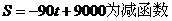 ,
,
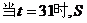 的最大值是
的最大值是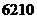 ……………………12分.
……………………12分.
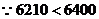 ,
,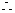 当
当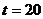 时,日销量额
时,日销量额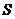 有最大值
有最大值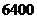 .
.
29、(江苏省常州市北郊中学2008届高三第一次模拟检测)设M是由满足下列条件的函数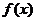 构成的集合:“①方程
构成的集合:“①方程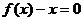 有实数根;②函数
有实数根;②函数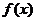 的导数
的导数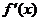 满足
满足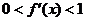 ”
”
(Ⅰ)判断函数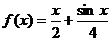 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(Ⅱ)若集合M中的元素具有下面的性质:“若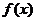 的定义域为D,则对于任意
的定义域为D,则对于任意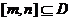 ,都存在
,都存在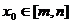 ,使得等式
,使得等式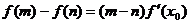 成立”
成立”
试用这一性质证明:方程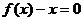 只有一个实数根;
只有一个实数根;
(Ⅲ)设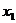 是方程
是方程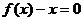 的实数根,求证:对于
的实数根,求证:对于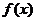 定义域中的任意的
定义域中的任意的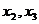 ,当
,当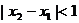 且
且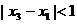 时,
时,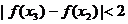
解:(Ⅰ)易证函数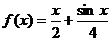 满足条件①②,因此
满足条件①②,因此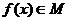
(Ⅱ)假设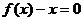 存在两个实根
存在两个实根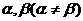 ,则
,则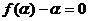 ,
,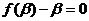 不妨设
不妨设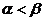 ,由题知存在实数
,由题知存在实数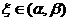 ,使得
,使得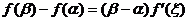 成立。∵
成立。∵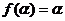 ,
,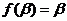 且
且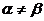 ,∴
,∴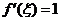 与已知矛盾,所以方程
与已知矛盾,所以方程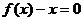 只有一个实数根
只有一个实数根
(Ⅲ) 不妨设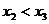 ,∵
,∵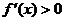 ,∴
,∴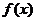 为增函数,∴
为增函数,∴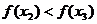 ,又∵
,又∵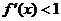 ∴函数
∴函数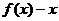 为减函数,∴
为减函数,∴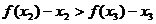 ,
,
∴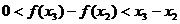 ,即
,即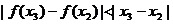 ,
,
∴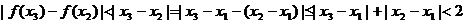
28、(黄家中学高08级十二月月考)设函数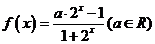 是R上的奇函数。
是R上的奇函数。
(Ⅰ)求a的值; (Ⅱ)求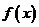 的反函数;
的反函数;
(Ⅲ)若k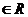 ,解不等式:
,解不等式: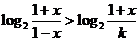
[解]:(Ⅰ): 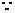 f(x) 是R上的奇函数,
f(x) 是R上的奇函数,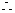 f(0)=0 得a=1
f(0)=0 得a=1
(Ⅱ) ∵y=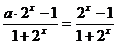 ∴y+y·2x=2x-1
∴y+y·2x=2x-1 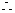 2x(y-1)=-1-y,2x=
2x(y-1)=-1-y,2x=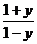
即:f-1(x)=log2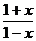 (-1<x<1)
(-1<x<1)
(Ⅲ) log2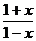 >log2
>log2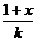 等价于
等价于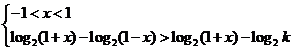
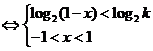
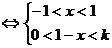
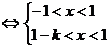
(i) -1<1-k<1,即0<k<2时,{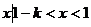 }
}
(ii) 1-k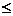 -1,即k
-1,即k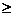 2时,{
2时,{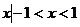 }
}
27、(湖北省荆门市2008届上期末)设函数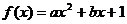 (
(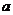 、
、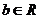 )
)
(1)若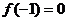 ,且对任意实数
,且对任意实数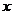 均有
均有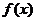
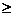 0成立,求实数
0成立,求实数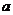 、
、 的值.
的值.
(2)在(1)的条件下,当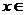 [-2,2]时,
[-2,2]时,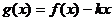 是单调函数,求实数
是单调函数,求实数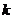 的取值范围.
的取值范围.
解
:(1)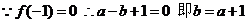
又对任意实数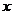 均有
均有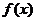
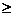 0成立
0成立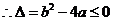 恒成立,即
恒成立,即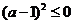 恒成立
恒成立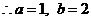 ………………………………6分
………………………………6分
(2)由(1)可知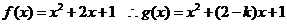
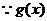 在
在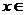 [-2,2]时是单调函数,
[-2,2]时是单调函数,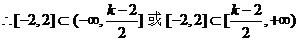
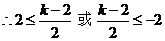 即实数
即实数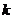 的取值范围为
的取值范围为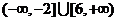
26、(湖北省黄冈市2007年秋季高三年级期末考试)已知函数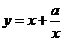 有如下性质:如果常数
有如下性质:如果常数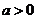 ,那么该函数在(0,
,那么该函数在(0,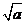 )上减函数,在
)上减函数,在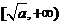 是增函数。
是增函数。
(1)如果函数 的值域为
的值域为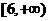 ,求
,求 的值;
的值;
(2)研究函数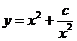 (常数
(常数 )在定义域的单调性,并说明理由;
)在定义域的单调性,并说明理由;
(3)对函数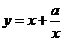 和
和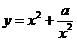 (常数
(常数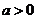 )作出推广,使它们都是你所推广的函数的特例。研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
)作出推广,使它们都是你所推广的函数的特例。研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
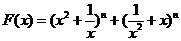 (n是正整数)在区间[
(n是正整数)在区间[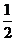 ,2]上的最大值和最小值(可利用你的研究结论)。
,2]上的最大值和最小值(可利用你的研究结论)。
解:(1)函数 的最小值是
的最小值是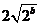 ,则
,则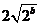 =6,
=6,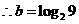 (2分)
(2分)
(2)设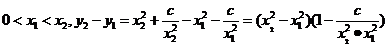
当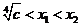 时,
时,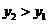 ,函数
,函数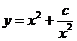 在
在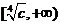 是增函数;(4分)
是增函数;(4分)
当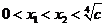 时,
时,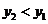 ,函数
,函数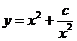 在
在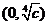 是减函数(5分)
是减函数(5分)
又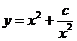 是偶函数,于是,该函数在
是偶函数,于是,该函数在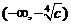 上是减函数,在
上是减函数,在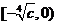
是增函数
(3)可以把函数推广为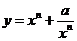 (常数
(常数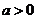 ),其中a是正整数。(7分)
),其中a是正整数。(7分)
当n是奇数时,函数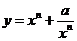 在
在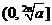 是减函数,在
是减函数,在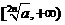 是增函数,在
是增函数,在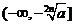 上是增函数,在
上是增函数,在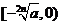 上是减函数;(9分)
上是减函数;(9分)
当n是奇数时,函数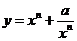 在
在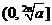 是减函数,在
是减函数,在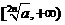 是增函数,在
是增函数,在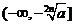 上是减函数,在
上是减函数,在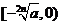 上是增函数;工协作(11分)
上是增函数;工协作(11分)
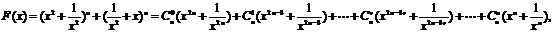
因此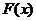 在
在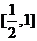 上减函数,在[1,2]上是增函数。
上减函数,在[1,2]上是增函数。
反以,当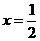 或
或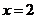 时,
时,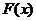 取得最大值
取得最大值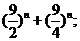 当x=1时
当x=1时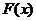 取得最小值。
取得最小值。
25、(湖北省黄冈市2007年秋季高三年级期末考试)某市的出租车的价格规定:起步费11元,可行3千米;3千米后按每千米2.1元计价,可再行7千米;以后每千米都按3.15元计价,设每一次乘车的车费由行车里程确定.
(1)请写出一次乘车的车费y元与行车的里程x千米的函数关系;
(2)计算如果一次乘车费为32元,那么汽车行程为多少千米?
(3)请问当行程为28千米时,请你设计一种乘车方案,使总费用最省.
解:(1)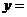 (4分)
(4分)
(2)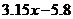 =32,
=32, 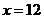 千米(6分)
千米(6分)
(3)当行程为3千米时,平均每千米为11/3元,显然当行程为10千米时,费用最省,即行程10千米时下车,重新上车计费,故当行程为28千米时,两次分别行程10千米时下车,重新上车计费,其费用为72.9元。
24、(河南省许昌市2008年上期末质量评估)设f(x)是定义在(0,1)上的函数,且满足:①对任意x∈(0,1),恒有f (x)>0;②对任意x1,x2∈(0,1),恒有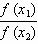 +
+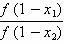 ≤2.
≤2.
(Ⅰ)求证:对任意x∈(0,1),恒有f(x)=f (1-x);
(Ⅱ)求证:对任意的x1、x2∈(0,1),恒有f (x1)=f (x2).

23、(广东省汕头市澄海区2008年第一学期期末考试)通过研究学生的学习行为,心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间。讲座开始时,学生兴趣激增;中间有一段不太长的时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散。分析结果和实验表明,用f(x)表示学生掌握和接受概念的能力,x表示提出概念和讲授概念的时间(单位:分),可有以下的关系式:
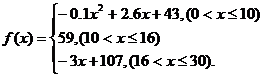
(1)开讲后多少分钟,学生的接受能力最强?能维持多少时间?
(2)一个数学难题,需要55(或以上)的接受能力,上课开始30分钟内, 求能达到该接受能力要求的时间共有多少分钟?
(3)如果每隔5分钟测量一次学生的接受能力,再计算平均值M=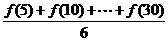 ,它能高于45吗?
,它能高于45吗?
解:(1)0<x≤10时,有f(x)=-0.1x2+2.6x+43=-0.1(x-13)2+59.9
故当0<x≤10时,时,f(x)递增,最大值为f(10)=-0.1×(-3)2+59.9=59;
显然,当16<x≤30时,f(x)递减,f(x)<-3×16+107=59.
因此,开讲后10分钟,学生达到最强的接受能力(值为59),
并维持6分钟; (5分)
(2) 依题意, 当0<x≤10时,令f(x)≥55,则(x-13)2≤49,
∴6≤x≤10; (7分)
当10<x≤16时,f(x)=59符合要求;(8分)
当16<x≤30时,令f(x)≥55,则x≤17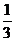 (9分)
(9分)
因此,学生达到(或超过)55的接受能力的时间为17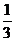 -6=11
-6=11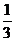 (分钟);(11分)
(分钟);(11分)
(3)f(5)=53.5, f(10)=59, f(15)=59, f(20)=47,f(25)=32, f(30)=17
所以M=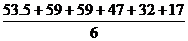 ≈44.6<45. (13分)
≈44.6<45. (13分)
故知平均值不能高于45.
22、(广东省佛山市2008年高三教学质量检测一)佛山某公司生产陶瓷,根据历年的情况可知,生产陶瓷每天的固定成本为14000元,每生产一件产品,成本增加210元.已知该产品的日销售量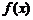 与产量
与产量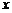 之间的关系式为
之间的关系式为
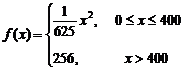 ,每件产品的售价
,每件产品的售价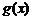 与产量
与产量 之间的关系式为
之间的关系式为
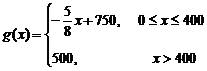 .
.
(Ⅰ)写出该陶瓷厂的日销售利润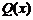 与产量
与产量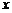 之间的关系式;
之间的关系式;
(Ⅱ)若要使得日销售利润最大,每天该生产多少件产品,并求出最大利润.
解:(Ⅰ)总成本为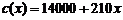 .
……1分
.
……1分
所以日销售利润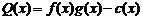
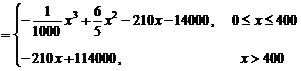 .
……6分
.
……6分
(Ⅱ)①当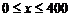 时,
时,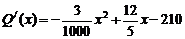 .
……7分
.
……7分
令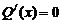 ,解得
,解得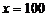 或
或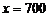 .
……8分
.
……8分
于是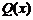 在区间
在区间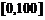 上单调递减,在区间
上单调递减,在区间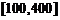 上单调递增,所以
上单调递增,所以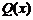 在
在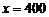 时取到最大值,且最大值为30000;
……10分
时取到最大值,且最大值为30000;
……10分
②当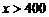 时,
时,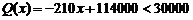 .
……12分
.
……12分
综上所述,若要使得日销售利润最大,每天该生产400件产品,其最大利润为30000元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com