
12.(文)已知向量m=(cos,cos),n=(cos,sin),且x∈[0,π],令函数f(x)=2a m·n+b.
(1)当a=1时,求f(x)的递增区间;
(2)当a<0时,f(x)的值域是[3,4],求a、b.
解:f(x)=2a m·n+b
=2a(cos2+sinx)+b
=2a(cosx+sinx+)+b
=a(sinx+cosx)+a+b
=asin(x+)+a+b.
(1)当a=1时,f(x)=sin(x+)+1+b.
令-+2kπ≤x+≤+2kπ,
得-π+2kπ≤x≤+2kπ(k∈Z),
又x∈[0,π],∴f(x)的递增区间为[0,].
(2)当a<0时,∵x∈[0,π],
∴x+∈[,],∴sin(x+)∈[-,1].
当sin(x+)=-时,f(x)=-a+a+b=b,
∴f(x)的最大值为b.
当sin(x+)=1时,f(x)=a+a+b=(1+)a+b.
∴f(x)的最小值为(1+)a+b.
∴解得a=1-,b=4.
(理)已知△ABC的外接圆半径为1,角A,B,C的对边分别为a,b,c.向量m=(a,4cosB),n=(cosA,b)满足m∥n.
(1)求sinA+sinB的取值范围;
(2)若实数x满足abx=a+b,试确定x的取值范围.
解:(1)因为m∥n,所以=,即ab=4cosAcosB.
因为△ABC的外接圆半径为1,由正弦定理,得
ab=4sinAsinB.
于是cosAcosB-sinAsinB=0,即cos(A+B)=0.
因为0<A+B<π.所以A+B=.故△ABC为直角三角形.
sinA+sinB=sinA+cosA=sin(A+),
因为<A+<,
所以<sin(A+)≤1,故1<sinA+sinB≤.
(2)x===.
设t=sinA+cosA(1<t≤),则2sinAcosA=t2-1,
x=,因为x′=<0,
故x=在(1,]上是单调递减函数.
所以≥.所以实数x的取值范围是[,+∞).
11.(2009·浙江高考)设向量a,b满足:|a|=3,|b|=4,a·b=0,以a,b,a-b的模为边长构成三角形,则它的边与半径为1的圆的公共点个数最多为 ( )
A.3 B.4 C.5 D.6
解析:当圆与三角形两边都相交时,有4个交点,本题新构造的三角形是直角三角形,其内切圆半径恰好为1.故它与半径为1的圆最多有4个交点.
答案:B
10.(2010·长郡模拟)已知| |=1,|
|=1,| |=,
|=, ·
· =0,
=0,
点C在∠AOB内,且∠AOC=30°,设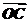 =m
=m +n
+n
(m,n∈R),则等于 ( )
A. B.3 C. D.
解析:| |=1,|
|=1,| |=,
|=, ·
· =0,
=0,
∴OA⊥OB,且∠OBC=30°,
又∵∠AOC=30°,∴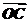
 ⊥
⊥ .
.
∴(m +n
+n )·(
)·( -
- )=0,
)=0,
∴-m 2+n
2+n 2=0,
2=0,
∴3n-m=0,
即m=3n,∴=3.
答案:B
9.已知平面向量a=(1,x),b=(2x+3,-x),x∈R.
(1)若a⊥b,求x的值;
(2)若a∥b,求|a-b|.
解:(1)若a⊥b,
则a·b=(1,x)·(2x+3,-x)
=1×(2x+3)+x(-x)=0.
整理得x2-2x-3=0,解得x=-1或x=3.
(2)若a∥b,则有1×(-x)-x(2x+3)=0,
即x(2x+4)=0,解得x=0或x=-2.
当x=0时,a=(1,0),b=(3,0),
∴|a-b|=|(1,0)-(3,0)|=|(-2,0)|
==2.
当x=-2时,a=(1,-2),b=(-1,2),
∴|a-b|=|(1,-2)-(-1,2)|=|(2,-4)|
==2.
|
题组四 |
平面向量数量积的综合应用 |

8.(2009·广东高考)若平面向量a,b满足|a+b|=1,a+b平行于x轴,b=(2,-1),则a=________.
解析:设a=(x,y),则a+b=(x+2,y-1)
由题意⇒
∴a=(-1,1)或a=(-3,1).
答案:(-1,1)或(-3,1)
7.已知向量a=(1,2),向量b=(x,-2),且a⊥(a-b),则实数x等于 ( )
A.-4 B.4 C.0 D.9
解析:∵a=(1,2),b=(x,-2),∴a-b=(1-x,4),
∵a⊥(a-b),∴a·(a-b)=0,∴1-x+8=0,∴x=9.
答案:D
6.设两个向量e1、e2满足|e1|=2,|e2|=1,e1、e2的夹角为60°,若向量2te1+7e2与向量e1+te2的夹角为钝角,求实数t的取值范围.
解:由已知,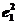 =|e1|2=4,
=|e1|2=4,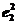 =|e2|2=1,
=|e2|2=1,
e1·e2=2×1×cos60°=1.
∴(2te1+7e2)·(e1+te2)=2t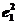 +(2t2+7)e1·e2+7t
+(2t2+7)e1·e2+7t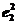
=2t2+15t+7.
由2t2+15t+7<0,得-7<t<-.
由2te1+7e2=λ(e1+te2)(λ<0),得,
∴.由于2te1+7e2与e1+te2的夹角为钝角,
故(2te1+7e2)·(e1+te2)<0且2te1+7e2≠λ(e1+te2)(λ<0),故t的取值范围是(-7,-)∪(-,-).
|
题组三 |
两向量的平行与垂直 |
5.在△ABC中, ·
· =3,△ABC的面积S∈[,],则
=3,△ABC的面积S∈[,],则 与
与 夹角的取值范围是
( )
夹角的取值范围是
( )
A.[,] B.[,] C.[,] D.[,]
解析:设〈 ·
· 〉=θ,由
〉=θ,由 ·
· =|
=| ||
|| |cosθ=3,得|
|cosθ=3,得| ||
|| |=,
|=,
∴S=| ||
|| |sinθ=××sinθ=tanθ.
|sinθ=××sinθ=tanθ.
由≤tanθ≤,得≤tanθ≤1,
∴≤θ≤.
答案:B
4.(2009·全国卷Ⅰ)设非零向量a、b、c满足|a|=|b|=|c|,a+b=c,则〈a,b〉=( )
A.150° B.120° C.60° D.30°
解析:(a+b)2=c2,a·b=-,cos〈a,b〉==-,〈a,b〉=120°.
答案:B
3.(2009·福建高考)设a,b,c为同一平面内具有相同起点的任意三个非零向量,且满足a与b不共线,a⊥c,|a|=|c|,则|b·c|的值一定等于 ( )
A.以a,b为两边的三角形的面积
B.以b,c为两边的三角形的面积
C.以a,b为邻边的平行四边形的面积
D.以b,c为邻边的平行四边形的面积
解析:设〈a,b〉=θ,θ∈(0,π),
 ∵〈a,c〉=,∴〈b,c〉=-θ,
∵〈a,c〉=,∴〈b,c〉=-θ,
以a,b为邻边的平行四边形面积为
|a||b|sinθ,而|b·c|=
=|b||c|sinθ,
又|a|=|c|,∴|b·c|=|a||b|sinθ.
答案:C
|
题组二 |
两向量的夹角问题 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com