
8.若平面向量a=(-1,2)与b的夹角是180°,且|b|=3,则b的坐标为 ( )
A.(3,-6) B.(-3,6)
C.(6,-3) D.(-6,3)
解析:由题意设b=λa=λ(-1,2).
由|b|=3得λ2=9.λ=±3.
因为a与b的夹角是180°.所以λ=-3.
答案:A
7.已知命题:“若k1a+k2b=0,则k1=k2=0”是真命题,则下面对a,b的判断正确
的是 ( )
A.a与b一定共线 B.a与b一定不共线
C.a与b一定垂直 D.a与b中至少有一个为0
解析:假设a与b共线,由已知得k1a=-k2b,如果a、b均为非零向量,与已知条件矛盾.如果a、b中至少有一个非零向量,明显的与已知矛盾,排除A、D.把k1a+k2b=0两边平方得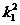 a2+
a2+ b2+2k1k2a·b=0,因为k1=k2=0,所以a·b不一定等于0,排除C.
b2+2k1k2a·b=0,因为k1=k2=0,所以a·b不一定等于0,排除C.
答案:B
6.(2010·鞍山模拟)已知复数z=1+i,则等于 ( )
A.2i B.-2i C.2 D.-2
解析:===2i.
答案:A
5.若在△ABC中,|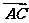 |=3,|
|=3,| |=5,|
|=5,|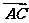 |=4,则|5
|=4,则|5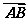 +
+ |= ( )
|= ( )
A.4 B.2 C.2 D.
解析:根据三边边长易知△ABC为直角三角形.
cos〈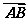 ,
, 〉=-.
〉=-.
∵|5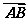 +
+ |2=
|2=
25|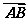 |2+|
|2+| |2+10|
|2+10|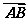 |·|
|·| |cos〈
|cos〈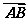 ,
, 〉=160.
〉=160.
∴|5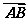 +
+ |=4.
|=4.
答案:A
4.如图,已知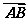
 =a,
=a,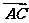 =b,
=b,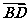 =3
=3 ,用a,b表示
,用a,b表示 ,则
,则 等于 ( )
等于 ( )

A.a+b B.a+b
C.a+b D.a+b
解析: =
=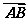 +
+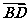 =
=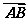 +
+
=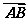 +(
+(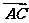 -
-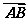 )=
)=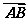 +
+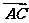 =a+b.
=a+b.
答案:B
3.(2010·利辛模拟)已知向量a=(2,3),b=(-1,2),若(ma+b)∥(a-2b),则实数m
( )
A. B.- C. D.
解析:ma+b=m(2,3)+(-1,2)=(2m-1,3m+2),
a-2b=(2,3)-2(-1,2)=(4,-1).
∵(ma+b)∥(a-2b)
∴1-2m=(3m+2)×4.
∴m=-.
答案:B
2.已知向量a=(-5,6),b=(6,5),则a与b ( )
A.垂直 B.不垂直也不平行
C.平行且同向 D.平行且反向
解析:已知向量a=(-5,6),b=(6,5),a·b=-30+30=0,则a与b垂直.
答案:A
1.(2009·天津高考)i是虚数单位,= ( )
A.1+2i B.-1-2i
C.1-2i D.-1+2i
解析:==-1+2i.
答案:D
12.复数z1=+(10-a2)i,z2=+(2a-5)i,若1+z2是实数,求实数a的值.
解:1+z2=+(a2-10)i++(2a-5)i
=(+)+[(a2-10)+(2a-5)]i
=+(a2+2a-15)i.
∵1+z2是实数,
∴a2+2a-15=0.
解得a=-5或a=3.
∵分母a+5≠0,
∴a≠-5,故a=3.
11.已知z1,z2为复数,(3+i)z1为实数,z2=,且|z2|=5,则z2= .
解析:z1=z2(2+i),
(3+i)z1=z2(2+i)(3+i)=z2(5+5i)∈R,
∵|z2|=5,
∴|z2(5+5i)|=50,∴z2(5+5i)=±50,
∴z2=±=±=±(5-5i).
答案:±(5-5i)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com