
(2010年北京海淀模拟)某学校研究性学习小组的学生通过调查,记录了该地区农事活动的时间表。分析表中信息,回答10~11题。
|
时间 |
6月~9月 |
9月~次年6月 |
6月~9月 |
|
农作物种植 |
玉米 |
小麦 |
玉米 |
10.该地区可能位于我国的 ( )
A.松嫩平原
B.黄淮海平原
C.鄱阳湖平原
D.准噶尔盆地的绿洲
11.该地区发展农业生产的主要限制性因素可能是 ( )
A.低温、冻害 B.地形、水源
C.旱涝、盐碱 D.光照、风沙
下图是表示某种产品生产和销售的一般模式。读图,回答7~9题。
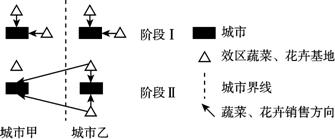
7.阶段Ⅰ花卉和蔬菜产区形成的主要区位因素是 ( )
A.地形平坦 B.气候优越
C.距城区近 D.水源充足
8.阶段Ⅱ花卉和蔬菜产区的区位变化主要是因为 ( )
A.城市用地规模的扩大
B.城市人口的增加
C.交通运输的便捷
D.城市居民收入增加
9.若甲城市在河北省,乙城市在广东省,则阶段Ⅱ运输量最大的季节是 ( )
A.春季 B.夏季
C.秋季 D.冬季
(2008年北京卷)读下图,回答5~6题。

5.该作物 ( )
A.种植期的早晚取决于气候条件
B.灌浆期的早晚取决于成土母质
C.收割期的早晚取决于农业政策
D.一个生产周期至少为8个月
6.该作物处于开花期时,正值 ( )
A.赤道正午太阳高度最大
B.地中海沿岸炎热干燥
C.中国东北平原昼长夜短
D.潘帕斯草原草木茂盛
据下图,回答3~4题。
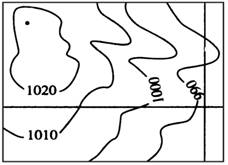
3.《水土保持法》规定,坡度大于25°的山地不得发展种植业。图示地区(比例尺为1?2000,tan 25°=0.47)适宜发展 ( )
A.林果业 B.种植业
C.园艺业 D.橡胶业
4.上图图示地区发展农业生产需要改造的因素是 ( )
A.土壤 地形 B.地形 水分
C.干旱 风沙 D.地形 植被
近年来,我国“温室无土栽培生产”在华北地区得以迅速推广,农业生产效率显著提高。据此回答1~2题。
1.该事实说明 ( )
A.没有土地也能进行农业生产
B.温室生产是提高农业生产效率的惟一手段
C.科技创新是发展农业的核心
D.“温室无土栽培生产”是解决华北地区农业缺水的重要途径
2.当前,我国华北的县、乡形成了专门生产蔬菜的农业基地,其产品供应范围相当广泛,这种基地形成的主要原因是 ( )
A.自然条件的改造和改良
B.作物生长季节的调整
C.国家政策、政府干预手段的影响
D.交通运输条件的改善和保鲜冷藏技术的发展
22.(本小题满分14分)已知△ABC的面积为S,满足≤S≤3,且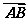 ·
· =6,
=6,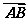 与
与 的夹角为θ.
的夹角为θ.
(1)求角θ的取值范围;
(2)求函数f(θ)=sin2θ+2sinθ·cosθ+3cos2θ的最小值.
解:(1)由题意知,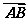 ·
· =|
=|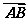 |·|
|·| |cosθ=6,
①
|cosθ=6,
①
S=|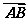 |·|
|·| |sin(π-θ)=|
|sin(π-θ)=|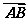 |·|
|·| |sinθ,
②
|sinθ,
②
由,得=tanθ,即3tanθ=S.
由≤S≤3,得≤3tanθ≤3,
即≤tanθ≤1.
又θ为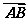 与
与 的夹角,
的夹角,
∴θ∈(0,π],∴θ∈[,].
(2)f(θ)=sin2θ+2sinθ·cosθ+3cos2θ
=1+sin2θ+2cos2θ
=2+sin2θ+cos2θ
=2+sin(2θ+).
∵θ∈[,],∴2θ+∈[,],
∴当2θ+=,即θ=时,f(θ)取得最小值为3.
21.(本小题满分12分)已知向量a=(cosx,sinx),b=(-cosx,cosx),c=(-1,0).
(1)若x=,求向量a,c的夹角;
(2)当x∈[,]时,求函数f(x)=2a·b+1的最大值.
解:(1)设a,c的夹角为θ,当x=时,
cos〈a,c〉==
=-cosx=-cos=cos.
∵0≤〈a,c〉≤π,∴〈a,c〉=.
(2)f(x)=2a·b+1=2(-cos2x+sinxcosx)+1
=2sinxcosx-(2cos2x-1)=sin2x-cos2x
=sin(2x-).
∵x∈[,],
∴2x-∈[,2π],
∴sin(2x-)∈[-1,],
∴当2x-=,即x=时,f(x)max=1.
20.(本小题满分12分)在△ABC中,角A、B、C所对的边长分别为a、b、c,已知向量m=(1,2sinA),n=(sinA,1+cosA),且满足m∥n,b+c=a.
(1)求角A的大小;
(2)求sin的值.
解:(1)∵m∥n,∴1+cosA=2sin2A,
即2cos2A+cosA-1=0,解得cosA=-1(舍去),cosA=.
又0<A<π,∴A=.
(2)∵b+c=a,
∴由正弦定理可得sinB+sinC=sinA=.
又C=π-(A+B)=-B,∴sinB+sin=,
即sinB+cosB=,∴sin=.
19.(本小题满分12分)已知向量a=(cos(-θ),sin(-θ)),b=(cos(-θ),sin(-θ)).
(1)求证:a⊥b;
(2)若存在不等于0的实数k和t,使x=a+(t2+3)b,
y=-ka+tb,满足x⊥y,试求此时的最小值.
解:(1)证明:∵a·b
=cos(-θ)·cos(-θ)+sin(-θ)·sin(-θ)
=sinθcosθ-sinθcosθ=0.
∴a⊥b.
(2)由x⊥y得:x·y=0,
即[a+(t2+3)b]·(-ka+tb)=0,
∴-ka2+(t3+3t)b2+[t-k(t2+3)]a·b=0,
∴-k|a|2+(t3+3t)|b|2=0.
又|a|2=1,|b|2=1,
∴-k+t3+3t=0,∴k=t3+3t.
∴==t2+t+3=(t+)2+.
故当t=-时,有最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com