
2、学生思考病毒的一般结构与特殊结构以及病毒的增殖过程。
学生回答:放线菌。
教师提问:放线菌在结构、繁殖方式上与细菌是否相同?如不同,请说出它们之间的异同?
师生共同活动:学生自主学习课本P75放线菌内容,在小组内讨论,教师巡视指导。
总结:(1)形态构造上放线菌是一类具有丝状分枝的单细胞原核生物。其分枝状的菌丝可分为:基内菌丝,伸入到培养基内部,色淡、较细,具有吸收营养和排泄代谢废物的功能;气生菌丝,在基内菌丝上不断向空间分化,伸展在空气中的较粗、颜色较深的菌丝;孢子丝,菌丝逐步成熟后,大部分气生菌丝分化为通过割裂方式产生成串的分生孢子的孢子丝,孢子丝形态多样,有杆形、波浪形、螺旋形等,且性状较稳定,是分类鉴定的重要指标。
(2)放线菌的繁殖方式:主要为孢子生殖。
(3)放线菌的生产应用:常用的抗生素,除青霉素和头孢霉素不是放线菌的产物外,多数抗生素都是放线菌的产物,如链霉素、红霉素等;除此之外,放线菌还能产生酶类和维生素;分解纤维素、石蜡、琼脂、橡胶等复杂有机物,提高土壤肥力,净化环境。
[教学目标巩固]
1、学生思考细菌的一般结构与特殊结构,并列表比较原核生物与真核生物在细胞结构上的异同。
2、病毒的增殖
师生互动:打开多媒体课件,学生观察并思考问题,教师结合问题分析。
增殖场所:
增殖过程:
教师呈示问题情景:同学们,有的细菌可使人体致病,但医疗部门为治疗这些疾病提供了大量的抗生素,你们知道这些抗生素主要是由什么微生物产生的呢?
出示病毒的结构示意图,请同学填空。
1、病毒的结构
基本结构:核衣壳
核酸:贮存病毒的全部遗传信息,控制着病毒的一切性状,如病毒的形态结构、致病性等。(一种病毒只含有一种核酸,DNA或RNA)
衣壳:化学本质:蛋白质,作用:保护病毒核酸、决定病毒特异性等
衣壳粒:电镜下能够看到的最小形态单位,通常由1~6个多肽分子组成。
病毒出现球形、杆形、蝌蚪形的直接原因?根本原因?
特殊结构:囊膜、刺突(如流感病毒)
呈示问题情景:某科学家在一实验时,以同位素示踪技术来研究病毒的增殖过程,他以32S标记噬菌体的衣壳的蛋白质,以31P标记噬菌体的核酸;当这样一个噬菌体去侵染一个以35S标记蛋白质、以32P标记核酸的细菌后,共释放出n个噬菌体,其中,含有31P标记核酸的噬菌体占总数的2/n,而且,所有病毒的衣壳中均只有35S标记蛋白质,这是为什么呢?
2、 细菌的结构与功能
(1)基本结构与功能
|
|
结构 |
化学本质 |
功能或应用 |
|
|
细胞壁 |
|
|
|
|
细胞膜 |
|
|
|
细胞质 |
基质 |
|
|
|
核糖体 |
|
|
|
|
质粒 |
|
|
|
|
贮藏性颗粒 |
|
|
|
|
核区 |
|
|
细胞壁:成分?作用?如何破坏细胞壁?(青霉素)
细胞膜:成分?作用?(有氧呼吸场所)
细胞质:含有的结构有?质粒的化学本质?上有哪些基因?存在部位?在基因工程中有何作用?所有的质粒都可作为基因工程的运载体吗?需具备哪些条件?
拟核:
(2)特殊结构和功能
|
结构 |
功能 |
举例说明何种细菌具有 |
|
荚膜 |
|
|
|
鞭毛 |
|
|
|
芽孢 |
|
|
出示:高中教材中涉及的细菌
乳酸菌、硝化细菌(代谢类型);肺炎双球菌S型、R型(遗传的物质基础);
结核杆菌和麻风杆菌(胞内寄生菌);根瘤菌、圆褐固氮菌(固氮菌);
大肠杆菌、枯草杆菌、土壤农杆菌(基因工程);苏云金芽孢杆菌(为抗虫棉提供抗虫基因);假单孢杆菌(分解石油的超级细菌);谷氨酸棒状杆菌、黄色短杆菌(微生物的代谢);链球菌(一般厌氧型);产甲烷杆菌(严格厌氧型)
提出问题:如何判断一种菌是细菌?(名称中带细菌字眼、形状上判断、特例)
1、 细菌的形态(球形/杆形/螺旋形)
出示:细菌的结构示意图,复习细菌的结构。
22.由曲线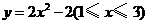 及直线
及直线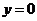 ,绕
,绕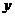 轴旋转所得的旋转体做容器,每秒钟向容器里注水
轴旋转所得的旋转体做容器,每秒钟向容器里注水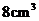 ,问几秒钟后能注满容器?(坐标的长度单位是cm)
,问几秒钟后能注满容器?(坐标的长度单位是cm)
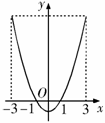 解:如图,底面是
解:如图,底面是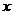 轴上
轴上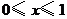 部分的线段绕
部分的线段绕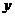 轴旋转所生成的圆,侧面是抛物线
轴旋转所生成的圆,侧面是抛物线 上
上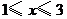 ,
,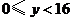 部分绕
部分绕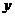 轴旋转所得的曲面.
轴旋转所得的曲面.
由 ,得
,得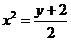 ,
,
注满容器时的体积为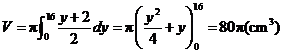 .
.
每秒注水8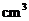 ,充满容器所需时间为
,充满容器所需时间为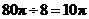 (秒).
(秒).
所以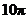 秒钟后能注满容器.
秒钟后能注满容器.
21.甲方是一农场,乙方是一工厂.由于乙方生产须占用甲方的资源,因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付甲方的情况下,乙方的年利润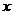 (元)与年产量
(元)与年产量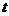 (吨)满足函数关系
(吨)满足函数关系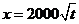 .若乙方每生产一吨产品必须赔付甲方
.若乙方每生产一吨产品必须赔付甲方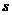 元(以下称
元(以下称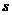 为赔付价格).
为赔付价格).
(1)将乙方的年利润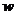 (元)表示为年产量
(元)表示为年产量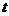 (吨)的函数,并求出乙方获得最大利润的年产量;
(吨)的函数,并求出乙方获得最大利润的年产量;
(2)甲方每年受乙生产影响的经济损失金额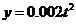 (元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格
(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格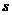 是多少?
是多少?
解:(1)因为赔付价格为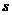 元/吨,所以乙方的实际年利润为
元/吨,所以乙方的实际年利润为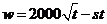 .
.
由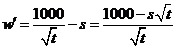 ,
,
令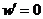 ,得
,得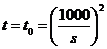 .
.
当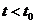 时,
时,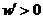 ;当
;当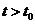 时,
时,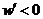 ,
,
所以 时,
时,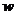 取得最大值.
取得最大值.
因此乙方取得最大年利润的年产量 为
为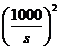 (吨);
(吨);
(2)设甲方净收入为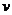 元,则
元,则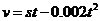 .
.
将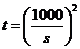 代入上式,得到甲方净收入
代入上式,得到甲方净收入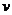 与赔付价格
与赔付价格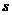 之间的函数关系式
之间的函数关系式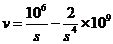 .
.
又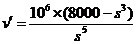 ,
,
令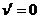 ,得
,得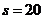 .
.
当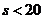 时,
时,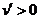 ;当
;当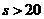 时,
时,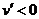 ,
,
所以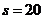 时,
时,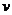 取得最大值.
取得最大值.
因此甲方应向乙方要求赔付价格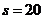 (元/吨)时,获最大净收入.
(元/吨)时,获最大净收入.
20.如图所示,求抛物线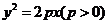 和过它上面的点
和过它上面的点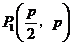 的切线的垂线所围成的平面图形的面积.
的切线的垂线所围成的平面图形的面积.
解:由题意令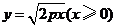 ,
,
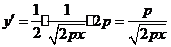 ,
,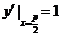 ,
,
所以过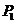 点且垂直于过
点且垂直于过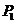 点的抛物线的切线的直线的斜率为
点的抛物线的切线的直线的斜率为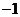 .
.
其方程为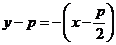 .
.
即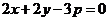 .
.
与抛物线方程联立消去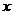 ,得
,得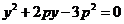 ,
,
解得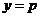 或
或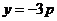 .
.
又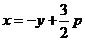 ,所以所求平面图形的面积为
,所以所求平面图形的面积为
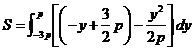
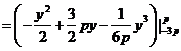
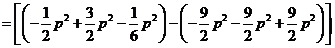
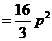 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com