3.运动员用双手握住竖直的竹竿匀速攀上和匀速下滑时，他所受到的摩擦力分别为f_上和f_下，那么它们的关系是(　)

A.f_上向上，f_下向下，f_上＝f_下

B.f_上向下，f_下向上，f_上＞f_下

C.f_上向上，f_下向上，f_上＝f_下

D.f_上向上，F_下向下，f_上＞f_下

2.如图所示，某一弹簧秤外壳的质量为m，弹簧及与弹簧相连的挂钩质量忽略不计，将其放在水平面上.现用两水平拉力F₁、F₂分别作用在与弹簧相连的挂钩和与外壳相连的提环上，则关于弹簧秤的示数，下列说法正确的是(　)

A.只有F₁＞F₂时，示数才为F₁

B.只有F₁＜F₂时，示数才为F₂

C.不论F₁、F₂关系如何，示数均为F₁

D.不论F₁、F₂关系如何，示数均为F₂

1.如图所示，竖直放置的轻弹簧一端固定在地面上，另一端与斜面体P连接，P与斜放的固定挡板MN接触且处于静止状态，弹簧处于竖直方向，则斜面体P此刻受到外力的个数可能为(　)

A.2　　B.3　　

C.4　　D.5

22、集合A＝{(x，y)｜y＝x²+mx+2}

　　B＝{(x，y)｜x－y+1＝0且0≤x≤2}若A∩B≠φ求实数m的范围。

21、设a≥0，f(x)＝x－1－ln²x+2alnx(x＞0)

(1)令F(x)＝xf’(x)，讨论F(x)在(0，+∞)内单调性并求极值。

(2)求证：当x＞0时，恒有x＞ln²x－2alnx+1。

20、f(x)＝x³－3ax+1(a≠0).

(1)求f(x)单调区间。

(2)若f(x)在x＝－1处有极值，直线y＝m与y＝f(x)的图象有三个不同交点，求m的取值范围。

19、函数f(x)＝2^x－1的反函数f^－1(x)，已知g(x)＝log₄(3x+1)。

(1)若f^－1(x)≤g(x)，求x的取值范围D。

(2)设函数H(x)＝g(x)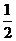－f^－1(x)，当x∈D时，求函数H(x)的值域。

18、(12分)已知定义在区间(0，+∞)上的函数f(x)满足f(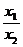)＝f(x₁)－f(x₂)，当x＞1时，f(x)＜0。

(1)求f(1)的值。

(2)判断f(x)单调性。

(3)若f(3)＝－1，解不等式｜f(|x|)｜＜2。

17、(10分)已知全集U＝R，集合A＝{x｜log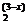≤2}，集合B＝{x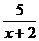｜≥1}

(1)求A、B。

(2)求(CuA)∩B。

16、函数y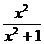＝的值域为　　　　　。