
+(200÷30)=146
所以,符合条件的数共有200-146=54(个)
点评:分析200个数分为两类,即满足题设条件的和不满足题设条件的两大类,而不满足条件的这一类标准明确而简单,可考虑用扣除法。
题型7:集合综合题
例11.(1999上海,17)设集合A={x||x-a|<2},B={x|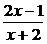 <1},若A
<1},若A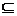 B,求实数a的取值范围。
B,求实数a的取值范围。
解:由|x-a|<2,得a-2<x<a+2,所以A={x|a-2<x<a+2}。
由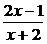 <1,得
<1,得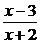 <0,即-2<x<3,所以B={x|-2<x<3}。
<0,即-2<x<3,所以B={x|-2<x<3}。
因为A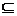 B,所以
B,所以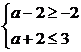 ,于是0≤a≤1。
,于是0≤a≤1。
点评:这是一道研究集合的包含关系与解不等式相结合的综合性题目。主要考查集合的概念及运算,解绝对值不等式、分式不等式和不等式组的基本方法。在解题过程中要注意利用不等式的解集在数轴上的表示方法.体现了数形结合的思想方法。
例12.已知{an}是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合A={(an,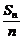 )|n∈N*},B={(x,y)|
)|n∈N*},B={(x,y)|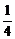 x2-y2=1,x,y∈R}。
x2-y2=1,x,y∈R}。
试问下列结论是否正确,如果正确,请给予证明;如果不正确,请举例说明:
(1)若以集合A中的元素作为点的坐标,则这些点都在同一条直线上;
(2)A∩B至多有一个元素;
(3)当a1≠0时,一定有A∩B≠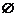 。
。
解:(1)正确;在等差数列{an}中,Sn=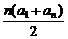 ,则
,则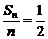 (a1+an),这表明点(an,
(a1+an),这表明点(an,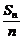 )的坐标适合方程y
)的坐标适合方程y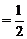 (x+a1),于是点(an,
(x+a1),于是点(an, 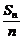 )均在直线y=
)均在直线y=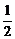 x+
x+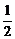 a1上。
a1上。
(2)正确;设(x,y)∈A∩B,则(x,y)中的坐标x,y应是方程组 的解,由方程组消去y得:2a1x+a12=-4(*),
的解,由方程组消去y得:2a1x+a12=-4(*),
当a1=0时,方程(*)无解,此时A∩B=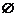 ;
;
当a1≠0时,方程(*)只有一个解x=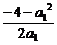 ,此时,方程组也只有一解
,此时,方程组也只有一解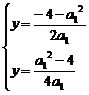 ,故上述方程组至多有一解。
,故上述方程组至多有一解。
∴A∩B至多有一个元素。
(3)不正确;取a1=1,d=1,对一切的x∈N*,有an=a1+(n-1)d=n>0,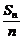 >0,这时集合A中的元素作为点的坐标,其横、纵坐标均为正,另外,由于a1=1≠0
>0,这时集合A中的元素作为点的坐标,其横、纵坐标均为正,另外,由于a1=1≠0 如果A∩B≠
如果A∩B≠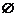 ,那么据(2)的结论,A∩B中至多有一个元素(x0,y0),而x0=
,那么据(2)的结论,A∩B中至多有一个元素(x0,y0),而x0=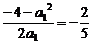 <0,y0=
<0,y0=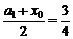 <0,这样的(x0,y0)
<0,这样的(x0,y0)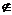 A,产生矛盾,故a1=1,d=1时A∩B=
A,产生矛盾,故a1=1,d=1时A∩B=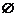 ,所以a1≠0时,一定有A∩B≠
,所以a1≠0时,一定有A∩B≠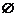 是不正确的。
是不正确的。
点评:该题融合了集合、数列、直线方程的知识,属于知识交汇题。
变式题:解答下述问题:
(Ⅰ)设集合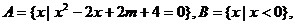 ,
,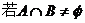 ,求实数m的取值范围.
,求实数m的取值范围.
 分析:关键是准确理解
分析:关键是准确理解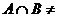 的具体意义,首先要从数学意义上解释
的具体意义,首先要从数学意义上解释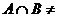
 的意义,然后才能提出解决问题的具体方法。
的意义,然后才能提出解决问题的具体方法。
解:
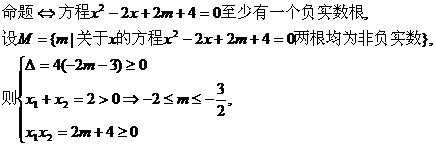
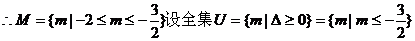
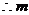 的取值范围是
的取值范围是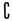 UM={m|m<-2}.
UM={m|m<-2}.

(解法三)设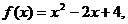 这是开口向上的抛物线,
这是开口向上的抛物线, ,则二次函数性质知命题又等价于
,则二次函数性质知命题又等价于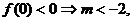
注意,在解法三中,f(x)的对称轴的位置起了关键作用,否则解答没有这么简单。
(Ⅱ)已知两个正整数集合A={a1,a2,a3,a4},
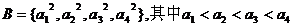
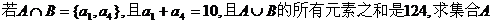 、B.
、B.
分析:命题中的集合是列举法给出的,只需要根据“交、并”的意义及元素的基本性质解决,注意“正整数”这个条件的运用,
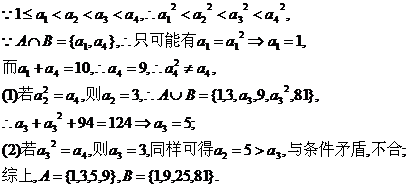
(Ⅲ)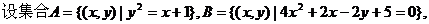
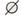

 分析:正确理解
分析:正确理解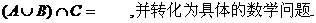
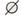
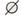
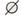 要使
要使 ,
,
由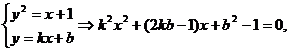
当k=0时,方程有解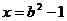 ,不合题意;
,不合题意;
当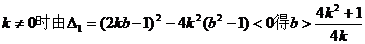 ①
①
又由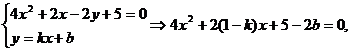
由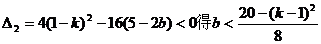 ②,
②,
由①、②得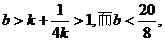
∵b为自然数,∴b=2,代入①、②得k=1
点评:这是一组关于集合的“交、并”的常规问题,解决这些问题的关键是准确理解问题条件的具体的数学内容,才能由此寻求解决的方法。
题型6:课标创新题
例13.七名学生排成一排,甲不站在最左端和最右端的两个位置之一,乙、丙都不能站在正中间的位置,则有多少不同的排法?
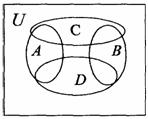 解:设集合A={甲站在最左端的位置},
解:设集合A={甲站在最左端的位置},
B={甲站在最右端的位置},
C={乙站在正中间的位置},
D={丙站在正中间的位置},
则集合A、B、C、D的关系如图所示,
∴不同的排法有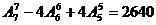 种.
种.
点评:这是一道排列应用问题,如果直接分类、分步解答需要一定的基本功,容易错,若考虑运用集合思想解答,则比较容易理解。上面的例子说明了集合思想的一些应用,在今后的学习中应注意总结集合应用的经验。
例14.A是由定义在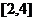 上且满足如下条件的函数
上且满足如下条件的函数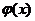 组成的集合:①对任意
组成的集合:①对任意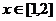 ,都有
,都有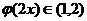 ; ②存在常数
; ②存在常数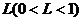 ,使得对任意的
,使得对任意的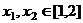 ,都有
,都有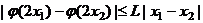
(1)设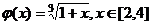 ,证明:
,证明: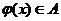
(2)设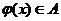 ,如果存在
,如果存在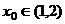 ,使得
,使得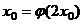 ,那么这样的
,那么这样的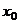 是唯一的;
是唯一的;
(3)设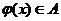 ,任取
,任取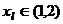 ,令
,令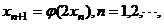 证明:给定正整数k,对任意的正整数p,成立不等式
证明:给定正整数k,对任意的正整数p,成立不等式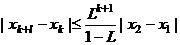 H。
H。
解:
对任意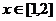 ,
,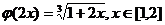 ,
,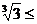
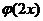
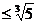 ,
,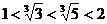 ,所以
,所以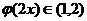
对任意的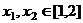 ,
,
 ,
,
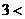
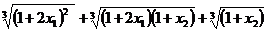 ,
,
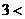 所以0<
所以0<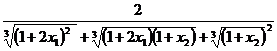
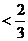 ,
,
令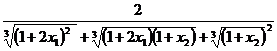 =
=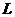 ,
,
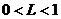 ,
,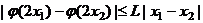
所以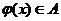
反证法:设存在两个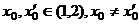 使得
使得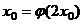 ,
,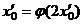 。
。
则由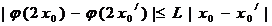 ,
,
得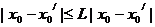 ,所以
,所以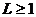 ,矛盾,故结论成立。
,矛盾,故结论成立。
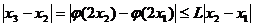 ,
,
所以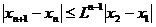
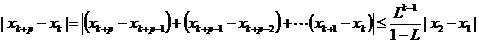

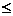
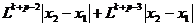 +…
+…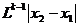
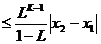 。
。
点评:函数的概念是在集合理论上发展起来的,而此题又将函数的性质融合在集合的关系当中,题目比较新颖
2、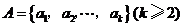 ,其中
,其中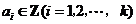 ,由
,由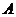 中的元素构成两个相应的集合:
中的元素构成两个相应的集合:
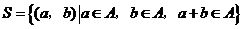 ,
,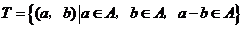 .其中
.其中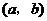 是有序数对,集合
是有序数对,集合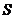 和
和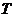 中的元素个数分别为
中的元素个数分别为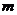 和
和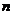 .若对于任意的
.若对于任意的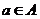 ,总有
,总有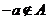 ,则称集合
,则称集合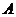 具有性质
具有性质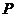 .
.
(I)对任何具有性质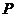 的集合
的集合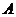 ,证明:
,证明: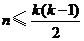 ;
;
(II)判断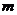 和
和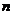 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
解:(I)证明:首先,由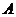 中元素构成的有序数对
中元素构成的有序数对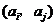 共有
共有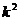 个.
个.
因为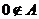 ,所以
,所以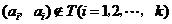 ;
;
又因为当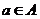 时,
时,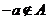 时,
时,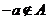 ,所以当
,所以当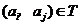 时,
时,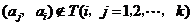 .
.
从而,集合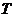 中元素的个数最多为
中元素的个数最多为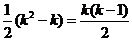 ,
,
即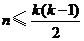 .
.
(II)解: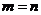 ,证明如下:
,证明如下:
(1)对于 ,根据定义,
,根据定义,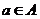 ,
,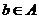 ,且
,且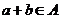 ,从而
,从而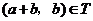 .
.
如果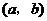 与
与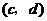 是
是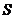 的不同元素,那么
的不同元素,那么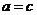 与
与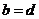 中至少有一个不成立,从而
中至少有一个不成立,从而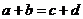 与
与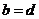 中也至少有一个不成立.
中也至少有一个不成立.
故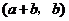 与
与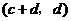 也是
也是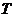 的不同元素.
的不同元素.
可见,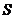 中元素的个数不多于
中元素的个数不多于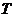 中元素的个数,即
中元素的个数,即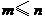 ,
,
(2)对于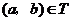 ,根据定义,
,根据定义,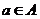 ,
,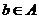 ,且
,且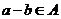 ,从而
,从而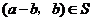 .如果
.如果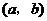 与
与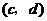 是
是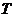 的不同元素,那么
的不同元素,那么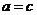 与
与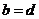 中至少有一个不成立,从而
中至少有一个不成立,从而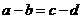 与
与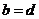 中也不至少有一个不成立,
中也不至少有一个不成立,
故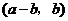 与
与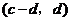 也是
也是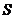 的不同元素.
的不同元素.
可见,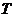 中元素的个数不多于
中元素的个数不多于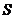 中元素的个数,即
中元素的个数,即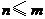 ,
,
由(1)(2)可知,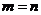 .
.
例9.向50名学生调查对A、B两事件的态度,有如下结果 赞成A的人数是全体的五分之三,其余的不赞成,赞成B的比赞成A的多3人,其余的不赞成;另外,对A、B都不赞成的学生数比对A、B都赞成的学生数的三分之一多1人。问对A、B都赞成的学生和都不赞成的学生各有多少人?
赞成A的人数是全体的五分之三,其余的不赞成,赞成B的比赞成A的多3人,其余的不赞成;另外,对A、B都不赞成的学生数比对A、B都赞成的学生数的三分之一多1人。问对A、B都赞成的学生和都不赞成的学生各有多少人?
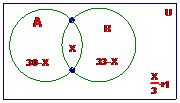 解:赞成A的人数为50×
解:赞成A的人数为50×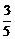 =30,赞成B的人数为30+3=33,如上图,记50名学生组成的集合为U,赞成事件A的学生全体为集合A;赞成事件B的学生全体为集合B。
=30,赞成B的人数为30+3=33,如上图,记50名学生组成的集合为U,赞成事件A的学生全体为集合A;赞成事件B的学生全体为集合B。
设对事件A、B都赞成的学生人数为x,则对A、B都不赞成的学生人数为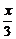 +1,赞成A而不赞成B的人数为30-x,赞成B而不赞成A的人数为33-x。依题意(30-x)+(33-x)+x+(
+1,赞成A而不赞成B的人数为30-x,赞成B而不赞成A的人数为33-x。依题意(30-x)+(33-x)+x+(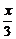 +1)=50,解得x=21。所以对A、B都赞成的同学有21人,都不赞成的有8人
+1)=50,解得x=21。所以对A、B都赞成的同学有21人,都不赞成的有8人 。
。
点评:在集合问题中,有一些常用的方法如数轴法取交并集,韦恩图法等,需要考生切实掌握。本题主要强化学生的这种能力。解答本题的闪光点是考生能由题目中的条件,想到用韦恩图直观地表示出来。本题难点在于所给的数量关系比较错综复杂,一时理不清头绪,不好找线索。画出韦恩图,形象地表示出各数量关系间的联系。
例10.求1到200这200个数中既不是2的倍数,又不是3的倍数,也不是5的倍数的自然数共有多少个?
 解:如图先画出Venn图,不难看出不符合条件
解:如图先画出Venn图,不难看出不符合条件
的数共有(200÷2)+(200÷3)+(200÷5)
2. 已知集合A={y|y2-(a2+a+1)y+a(a2+1)>0},B={y|y2-6y+8≤0},若A∩B≠φ,则实数a的取值范围为( ).
分析:解决数学问题的思维过程,一般总是从正面入手,即从已知条件出发,经过一系列的推理和运算,最后得到所要求的结论,但有时会遇到从正面不易入手的情况,这时可从反面去考虑.从反面考虑问题在集合中的运用主要就是运用补集思想.本题若直接求解,情形较复杂,也不容易得到正确结果,若我们先考虑其反面,再求其补集,就比较容易得到正确的解答.
解:由题知可解得A={y|y>a2+1或y<a}, B={y|2≤y≤4},我们不妨先考虑当A∩B=φ时a的范围.如图
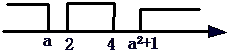
由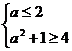 ,得
,得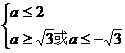
∴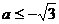 或
或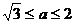 .
.
即A∩B=φ时a的范围为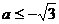 或
或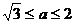 .而A∩B≠φ时a的范围显然是其补集,从而所求范围为
.而A∩B≠φ时a的范围显然是其补集,从而所求范围为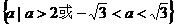 .
.
评注:一般地,我们在解时,若正面情形较为复杂,我们就可以先考虑其反面,再利用其补集,求得其解,这就是“补集思想”.
例4.已知全集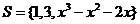 ,A={1,
,A={1,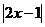 }如果
}如果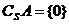 ,则这样的实数
,则这样的实数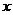 是否存在?若存在,求出
是否存在?若存在,求出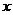 ,若不存在,说明理由
,若不存在,说明理由
解:∵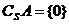 ;
;
∴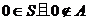 ,即
,即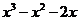 =0,解得
=0,解得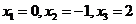
当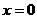 时,
时,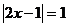 ,为A中元素;
,为A中元素;
当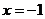 时,
时,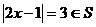
当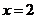 时,
时,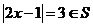
∴这样的实数x存在,是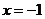 或
或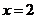 。
。
另法:∵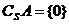
∴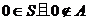 ,
,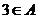
∴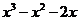 =0且
=0且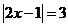
∴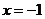 或
或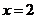 。
。
点评:该题考察了集合间的关系以及集合的性质。分类讨论的过程中“当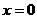 时,
时,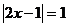 ”不能满足集合中元素的互异性。此题的关键是理解符号
”不能满足集合中元素的互异性。此题的关键是理解符号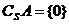 是两层含义:
是两层含义: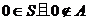 。
。
变式题:已知集合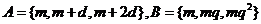 ,
,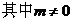 ,
,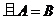 ,求
,求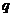 的值。
的值。
解:由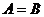 可知,
可知,
(1)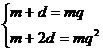 ,或(2)
,或(2)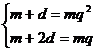
解(1)得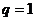 ,
,
解(2)得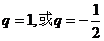 ,
,
又因为当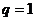 时,
时,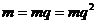 与题意不符,
与题意不符,
所以,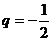 。
。
题型3:集合的运算
例5.(2008年河南省上蔡一中高三月考)已知函数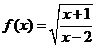 的定义域集合是A,函数
的定义域集合是A,函数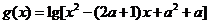 的定义域集合是B
的定义域集合是B
(1)求集合A、B
(2)若A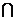 B=B,求实数
B=B,求实数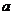 的取值范围.
的取值范围.
解
(1)A=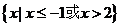
B=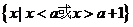
(2)由A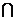 B=B得A
B=B得A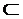 B,因此
B,因此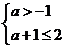
所以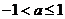 ,所以实数
,所以实数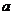 的取值范围是
的取值范围是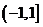
例6.(2009宁夏海南卷理)已知集合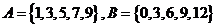 ,则
,则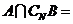 ( )
( )
A.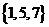 B.
B.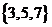
C.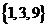 D.
D.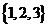
答案 A
解析 易有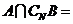
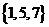 ,选A
,选A
点评:该题考察了集合的交、补运算。
题型4:图解法解集合问题
例7.(2009年广西北海九中训练)已知集合M=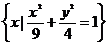 ,N=
,N=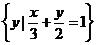 ,则
,则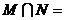 ( )
( )
A.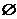 B.
B.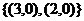
C.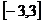 D.
D.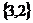
答案 C
例8.湖南省长郡中学2008届高三第六次月考试卷数学(理)试卷
设全集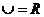 ,函数
,函数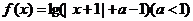 的定义域为A,集合
的定义域为A,集合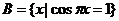 ,若
,若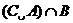 恰好有2个元素,求a的取值集合。
恰好有2个元素,求a的取值集合。
解: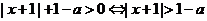
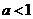 时,
时,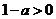 ∴
∴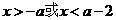
∴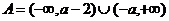
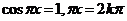 ,∴
,∴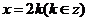
∴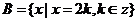
当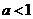 时,
时,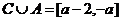 在此区间上恰有2个偶数。
在此区间上恰有2个偶数。
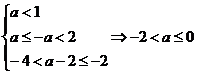
题型1:集合的概念
(2009湖南卷理)某班共30人,其中15人喜爱篮球运动,10人喜爱兵乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为_12__
答案 :12
解析 设两者都喜欢的人数为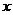 人,则只喜爱篮球的有
人,则只喜爱篮球的有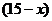 人,只喜爱乒乓球的有
人,只喜爱乒乓球的有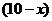 人,由此可得
人,由此可得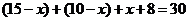 ,解得
,解得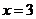 ,所以
,所以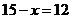 ,即
所求人数为12人。
,即
所求人数为12人。 

例1.(2009广东卷理)已知全集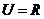 ,集合
,集合 和
和
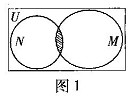
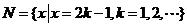 的关系的韦恩(Venn)图如图1所示,则阴影部分所示的集合的元素共有 ( )
的关系的韦恩(Venn)图如图1所示,则阴影部分所示的集合的元素共有 ( )
A. 3个 B. 2个
C. 1个 D. 无穷多个
答案 B
解析
由 得
得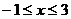 ,则
,则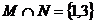 ,有2个,选B.
,有2个,选B.
例2.(2009山东卷理)集合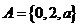 ,
,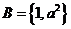 ,若
,若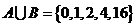 ,则
,则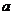 的值
的值
为 ( )
A.0 B.1 C.2 D.4
答案 D
解析
∵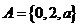 ,
,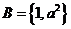 ,
,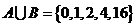 ∴
∴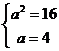 ∴
∴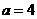 ,故选D.
,故选D.
[命题立意]:本题考查了集合的并集运算,并用观察法得到相对应的元素,从而求得答案,本题属于容易题.
题型2:集合的性质
例3.(2009山东卷理)集合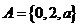 ,
,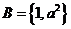 ,若
,若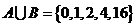 ,则
,则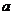 的值为 ( )
的值为 ( )
A.0 B.1 C.2 D.4
答案 D
解析
∵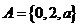 ,
,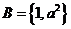 ,
,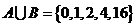 ∴
∴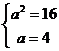 ∴
∴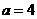 ,故选D.
,故选D.
[命题立意]:本题考查了集合的并集运算,并用观察法得到相对应的元素,从而求得答案,本题属于容易题.
随堂练习
1.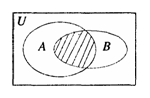 ( 广东地区2008年01月份期末试题汇编)设全集U=R,A={x∈N︱1≤x≤10},B={ x∈R︱x 2+
x-6=0},则下图中阴影表示的集合为 ( )
( 广东地区2008年01月份期末试题汇编)设全集U=R,A={x∈N︱1≤x≤10},B={ x∈R︱x 2+
x-6=0},则下图中阴影表示的集合为 ( )
A.{2} B.{3}
C.{-3,2} D.{-2,3}
5.集合的简单性质:
(1)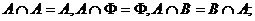
(2)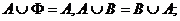
(3)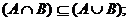
(4)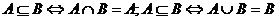 ;
;
(5)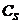 (A∩B)=(
(A∩B)=(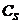 A)∪(
A)∪(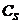 B),
B),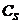 (A∪B)=(
(A∪B)=(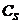 A)∩(
A)∩(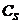 B)。
B)。
4.交集与并集:
(1)一般地,由属于集合A且属于集合B的元素所组成的集合,叫做集合A与B的交集。交集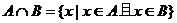 。
。
(2)一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集。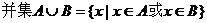

注意:求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法。
3.全集与补集:
(1)包含了我们所要研究的各个集合的全部元素的集合称为全集,记作U;
(2)若S是一个集合,A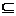 S,则,
S,则,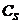 =
=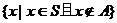 称S中子集A的补集;
称S中子集A的补集;
(3)简单性质:1)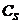 (
(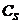 )=A;2)
)=A;2)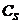 S=
S=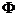 ,
,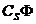 =S
=S
2.集合的包含关系:
(1)集合A的任何一个元素都是集合B的元素,则称A是B的子集(或B包含A),记作A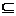 B(或
B(或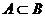 );
);
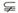 集合相等:构成两个集合的元素完全一样。若A
集合相等:构成两个集合的元素完全一样。若A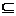 B且B
B且B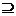 A,则称A等于B,记作A=B;若A
A,则称A等于B,记作A=B;若A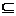 B且A≠B,则称A是B的真子集,记作A B;
B且A≠B,则称A是B的真子集,记作A B;
(2)简单性质:1)A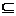 A;2)
A;2)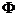
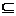 A;3)若A
A;3)若A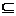 B,B
B,B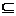 C,则A
C,则A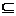 C;4)若集合A是n个元素的集合,则集合A有2n个子集(其中2n-1个真子集);
C;4)若集合A是n个元素的集合,则集合A有2n个子集(其中2n-1个真子集);
1.集合:某些指定的对象集在一起成为集合
(1)集合中的对象称元素,若a是集合A的元素,记作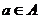 ;若b不是集合A的元素,记作
;若b不是集合A的元素,记作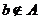 ;
;
(2)集合中的元素必须满足:确定性、互异性与无序性;
确定性:设A是一个给定的集合,x是某一个具体对象,则或者是A的元素,或者不是A的元素,两种情况必有一种且只有一种成立;
互异性:一个给定集合中的元素,指属于这个集合的互不相同的个体(对象),因此,同一集合中不应重复出现同一元素;
无序性:集合中不同的元素之间没有地位差异,集合不同于元素的排列顺序无关;
(3)表示一个集合可用列举法、描述法或图示法;
列举法:把集合中的元素一一列举出来,写在大括号内;
描述法:把集合中的元素的公共属性描述出来,写在大括号{}内。
具体方法:在大括号内先写上表示这个集合元素的一般符号及取值(或变化)范围,再画一条竖线,在竖线后写出这个集合中元素所具有的共同特征。
注意:列举法与描述法各有优点,应该根据具体问题确定采用哪种表示法,要注意,一般集合中元素较多或有无限个元素时,不宜采用列举法。
(4)常用数集及其记法:
非负整数集(或自然数集),记作N;
正整数集,记作N*或N+;
整数集,记作Z;
有理数集,记作Q;
实数集,记作R。
有关集合的高考试题,考查重点是集合与集合之间的关系,近年试题加强了对集合的计算化简的考查,并向无限集发展,考查抽象思维能力,在解决这些问题时,要注意利用几何的直观性,注意运用Venn图解题方法的训练,注意利用特殊值法解题,加强集合表示方法的转换和化简的训练。考试形式多以一道选择题为主,分值5分。
预测2010年高考将继续体现本章知识的工具作用,多以小题形式出现,也会渗透在解答题的表达之中,相对独立。具体题型估计为:
(1)题型是1个选择题或1个填空题;
(2)热点是集合的基本概念、运算和工具作用
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com