
7.橡皮筋也像弹簧一样,在弹性限度内,伸长量x与弹力F成正比,即F=kx,k的值与橡皮筋未受到拉力时的长度L、横截面积S有关,理论与实践都表明k=Y,其中Y是一个由材料决定的常数,材料力学上称之为杨氏模量.
(1)在国际单位制中,杨氏模量Y的单位应该是 ( )
A.N B.m C.N/m D.Pa
(2)有一段横截面是圆形的橡皮筋,应用如图实-3-14
所示的实验装置可以测量出它的杨氏模量Y的值.首先
利用测量工具a测得橡皮筋的长度L=20.00 cm,利用
测量工具b测得橡皮筋未受到拉力时的直径D=
6.(2008·北京高考)某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0;弹簧下端挂一个50 g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50 g的砝码时,指针指示的刻度数值记作L2;……;挂七个50 g的砝码时,指针指示的刻度数值记作L7.
(1)下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是 和 .
代表
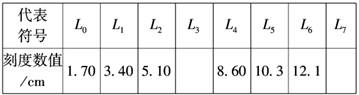
(2)实验中,L3和L7两个值还没有测定,请你根据图实-3-13将这两个测量值填入上表中.

图实-3-13
(3)为了充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90 cm,d2=L5-L1=6.90 cm,d3=L6-L2=7.00 cm.
请你给出第四个差值:d4= = cm.
(4)根据以上差值,可以求出每增加50 g砝码的弹簧平均伸长量ΔL.ΔL用d1、d2、d3、d4表示的式子为:ΔL= ,代入数据解得ΔL= cm.
(5)计算弹簧的劲度系数k= N/m.(g取9.8 m/s2)
解析:(1)L5、L6两组数据在读数时均没有估读值.
(2)根据表格已知读数,刻度尺上端的刻度数小,因而L3=6.85 cm,L7=14.05 cm.
(3)题中三组数据在寻求多挂4个砝码形成的长度差,故d4=L7-L3=(14.05-6.85)cm=7.20 cm.
(4)每增加4个砝码弹簧的平均伸长量ΔL1=,则每增加1个砝码弹簧的平均伸长量ΔL==,代入数据求得ΔL=1.75 cm.
(5)由(3)(4)可知,弹力F和弹簧伸长量ΔL成正比,即满足F=kΔL,代入数据
k== N/m=28 N/m.
答案:(1)L5 L6 (2)6.85 14.05
(3)L7-L3 7.20
(4) 1.75 (5)28
5.某同学用如图实-3-11所示装置做“探究弹力和弹簧伸长
关系”的实验.他先测出不挂钩码时弹簧下端指针所指的标
尺刻度,然后在弹簧下端挂上钩码,并逐个增加钩码,测
出指针所指的标尺刻度,所得数据列表如下:(g取9.8 m/s2) 图实-3-11
钩码质量
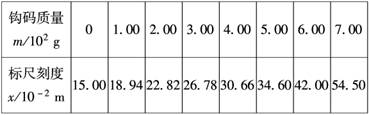
(1)根据所测数据,在图实-3-12所示的坐标纸上作出弹簧指针所指的标尺的刻度x与钩码质量m的关系曲线.
(2)根据所测得的数据和关系曲线可以判断,在 N范围内弹力大小与弹簧伸长关系满足胡克定律,这种规格的弹簧的劲度系数为 N/m.
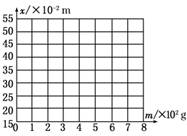
图实-3-12
解析:(1)根据题目中所测量的数据进行描点,然后用平滑的曲线(或直线)连接各点,在连接时应让尽量多的点落在线上,偏差比较大的点舍去,不在线上的点尽量均匀分布在线的两侧,如图所示.
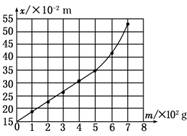
(2)根据所画图象可以看出,当m≤5.00×102 g=0.5 kg时,标尺刻度x与钩码质量m成一次函数关系,所以在F≤4.9 N范围内弹力大小与弹簧伸长关系满足胡克定律,由胡克定律F=kΔx可知,图线斜率的大小在数值上等于弹簧的劲度系数k,即
k===25.0 N/m.
答案:(1)见解析 (2)0-4.9 25.0
4.用如图实-3-10甲所示的装置测定弹簧的劲度系数,被测弹簧一端固定于A点,另一端B用细绳绕过定滑轮挂钩码,旁边竖直固定一最小刻度为mm的刻度尺,当挂两个钩码时,绳上一定点P对应刻度如图实-3-10乙中ab虚线所示,再增加一个钩码后,P点对应刻度如图实-3-10乙中cd虚线所示,已知每个钩码质量为50 g,重力加速度g=9.8 m/s2,则被测弹簧的劲度系数为 N/m.挂三个钩码时弹簧的形变量为 cm.
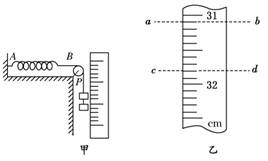
图实-3-10
解析:对钩码进行受力分析,根据平衡条件和胡克定律,得
2mg=k(l-l0)
3mg=k(l′-l0)
则k== N/m=70 N/m
挂三个钩码时,可列方程
(m+m+m)g=kΔx′
Δx′== m
=2.10×10-2 m=2.10 cm.
 答案:70 2.10
答案:70 2.10
3.(2010·安徽省两地三校联考)某同学在研究性学习中,利用所学的知识解决了如下问题:一轻弹簧竖直悬挂于某一深度为h=25.0 cm,且开口向下的小筒中(没有外力作用时弹簧的下部分位于筒内,但测力计可以同弹簧的下端接触),如图实-3-9甲所示,如果本实验的长度测量工具只能测量出筒的下端弹簧的长度l,现要测出弹簧的原长l0和弹簧的劲度系数,该同学通过改变l而测出对应的弹力F,作出F-l变化的图线如图乙所示,则弹簧的劲度系数为 N/m,弹簧的原长l0= m.
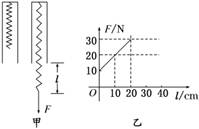
图实-3-9
解析:由胡克定律可得F=kx=k(h+l-l0)=k(h-l0)+kl.因此F-l图线的斜率即为弹簧的劲度系数k= N/m=100 N/m,k(h-l0)=10 N,得l0=0.15 m.
答案:100 0.15
2.(2010·临沂质检)如图实-3-8甲所示,一个弹簧一端固定在传感器上,传感器与电脑相连.当对弹簧施加变化的作用力(拉力或压力)时,在电脑上得到了弹簧形变量与弹簧产生的弹力大小的关系图象,如图实-3-8乙所示.则下列判断正确的是 ( )
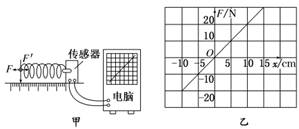
图实-3-8
A.弹簧产生的弹力和弹簧的长度成正比
B.弹力增加量与对应的弹簧长度的增加量成正比
C.该弹簧的劲度系数是200 N/m
D.该弹簧受到反向压力时,劲度系数不变
解析:由图乙知,F-x是一个过原点的直线,k= N/m=200 N/m,可知A错,B、C、D正确.
答案:BCD
1.(2009·广东理基)一个实验小组在“探究弹力和弹簧伸长的
关系”的实验中,使用两条不同的轻质弹簧a和b,得到弹
力与弹簧长度关系的图象如图实-3-7所示.下列表述正确的
是 ( ) 图实-3-7
A.a的原长比b的长
B.a的劲度系数比b的大
C.a的劲度系数比b的小
D.测得的弹力与弹簧的长度成正比
解析:图象的横轴截距表示弹簧的原长,A错误;图象的斜率表示弹簧的劲度系数,B正确,C错误;图象不过原点,D错误.
答案:B
(15) 设数列{an}的首项a1=a≠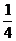 ,且
,且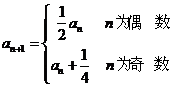 ,
,
记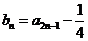 ,n==l,2,3,…·.
,n==l,2,3,…·.
(I)求a2,a3;
(II)判断数列{bn}是否为等比数列,并证明你的结论;
(III)求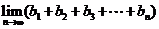
(16) 数列{an}的前n项和为Sn,且a1=1,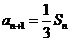 ,n=1,2,3,……,求
,n=1,2,3,……,求
(I)a2,a3,a4的值及数列{an}的通项公式;
(II)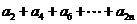 的值.
的值.
(17) 已知{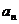 }是公比为q的等比数列,且
}是公比为q的等比数列,且 成等差数列.
成等差数列.
(Ⅰ)求q的值;
(Ⅱ)设{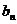 }是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
.
(18) 已知定义在R上的函数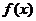 和数列
和数列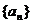 满足下列条件:
满足下列条件:
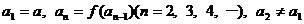 ,
,
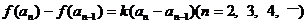 ,其中a为常数,k为非零常数.
,其中a为常数,k为非零常数.
(Ⅰ)令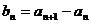
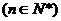 ,证明数列
,证明数列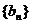 是等比数列;
是等比数列;
(Ⅱ)求数列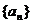 的通项公式;
的通项公式;
(Ⅲ)当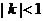 时,求
时,求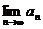 .
.
(11) 在等差数列{an}中,a1>0,a5=3a7,前n项和为Sn,若Sn取得最大值,则n= .
(12) 在等差数列{an}中,前n项和为Sn,若S19=31,S31=19,则S50的值是______
(13)在等比数列{an}中,若a9·a11=4,则数列{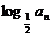 }前19项之和为_______
}前19项之和为_______
(14)若a>0,且a≠1, 则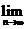
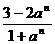 的值是
.
的值是
.
(1) 已知等差数列{an}的前n项和为Sn,且S4=3,S8=7,则S12的值是 ( )
A 8 B 11 C 12 D 15
(2) 已知数列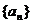 满足
满足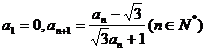 ,则
,则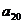 = ( )
= ( )
A 0 B 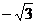 C
C 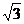 D
D 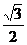
(3) 数列1,(1+2),(1+2+22),…,( 1+2+22+…+2n-1+…)的前n项和是 ( )
A 2n B 2n-2 C 2n+1- n -2 D n·2n
(4) 从集合{1,2,3,4,5,6,7,8,9,10}中任选三个不同的数,如果这三个数经过适当的排列成等差数列,则这样的等差数列一共有 ( )
A 20个 B 40个 C 10个 D 120个
(5) 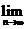
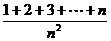 =
( )
=
( )
A 2
B 4 C 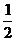 D
0
D
0
(6) 如果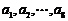 为各项都大于零的等差数列,公差
为各项都大于零的等差数列,公差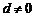 ,则
( )
,则
( )
A 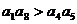 B
B 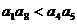 C
C 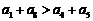 D
D 
(7)已知等差数列{an}与{bn}的前n项和分别为Sn与Tn, 若 , 则
, 则
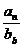 的值是
( )
的值是
( )
A 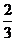 B
B 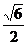 C
C 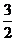 D
D 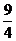
(8) 
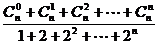 的值是
(
)
的值是
(
)
A 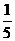 B
B
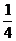 C
C
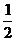 D
D 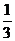
(9) 已知数列{log2(an-1)}(n∈N*)为等差数列,且a1=3,a2=5,则
 =
(
)
=
(
)
A 2 B 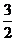 C 1 D
C 1 D 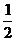
(10) 已知数列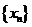 满足
满足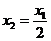 ,
,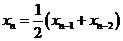 ,
,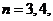 ….若
….若 ,则 ( )
,则 ( )
A 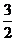 B3
C4
D5
B3
C4
D5
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com