
考点1. 气体压强的分析与计算
剖析:
(1)封闭气体有两种情况:一是平衡状态系统中的封闭气体,二是变速运动系统中的封闭气体。
(2)封闭气体压强的计算方法:选与气体接触的液柱(或活塞、汽缸)为研究对象,进行受力分析;再根据运动状态列出相应的平衡方程或牛顿第二定律方程,从而求出压强。
(3)气体压强的计算常要用到以下知识
①若液面与外界大气相接触,则液面下h深处压强p=p0+ρgh,h为坚直深度。
②与外界相通时,容器内的压强等于外界气压;用细管相连通的两容器,平衡时两边气体的压强相等。
③连通器原理:在连通器中,同一种液体(中间不间断)的同一水平面上压强相等。
④帕斯卡定律:加在密闭、静止液体(或气体)上的压强,能够大小不变地由液体(或气体)向各个方向传递。
|
 [例题1]图13-3-1中气缸静止在水平面上,缸内用活塞封闭一定质量的空气。活塞的的质量为m,横截面积为S,下表面与水平方向成θ角,若大气压为p0,求封闭气体的压强p
[例题1]图13-3-1中气缸静止在水平面上,缸内用活塞封闭一定质量的空气。活塞的的质量为m,横截面积为S,下表面与水平方向成θ角,若大气压为p0,求封闭气体的压强p
 解析:以活塞为对象进行受力分析,关键是气体对活塞的压力方向应该垂直与活塞下表面而向斜上方,与竖直方向成θ角,接触面积也不是S而是S1=S/cosθ。因此竖直方向受力平衡方程为:pS1cosθ=mg+p0S,得p=p0+mg/S。结论跟θ角的大小无关。
解析:以活塞为对象进行受力分析,关键是气体对活塞的压力方向应该垂直与活塞下表面而向斜上方,与竖直方向成θ角,接触面积也不是S而是S1=S/cosθ。因此竖直方向受力平衡方程为:pS1cosθ=mg+p0S,得p=p0+mg/S。结论跟θ角的大小无关。
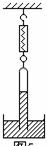 [变式训练1]如图12-3-2所示,一端封闭的玻璃管中有一些空气和一段水银柱,将它倒立在水银槽中,上端与弹簧秤相连,则弹簧秤的示数为
[变式训练1]如图12-3-2所示,一端封闭的玻璃管中有一些空气和一段水银柱,将它倒立在水银槽中,上端与弹簧秤相连,则弹簧秤的示数为
 .玻璃管的重力和弹簧秤的重力之和
.玻璃管的重力和弹簧秤的重力之和
 .玻璃管的重力和露出液面的那段水银柱的重力之和
.玻璃管的重力和露出液面的那段水银柱的重力之和
|
 .大气向上的压力减去玻璃管的重力
.大气向上的压力减去玻璃管的重力
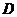 .玻璃管、弹簧秤和露出液面的那段水银柱三者重力之和
.玻璃管、弹簧秤和露出液面的那段水银柱三者重力之和
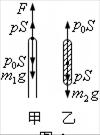 解析:设大气压强为
解析:设大气压强为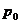 ,玻璃管内被封闭空气的压强为
,玻璃管内被封闭空气的压强为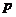 ,将玻璃管和露出液面的那段水银柱进行受力分析分别如图12-3-3甲、乙所示,由平衡条件得
,将玻璃管和露出液面的那段水银柱进行受力分析分别如图12-3-3甲、乙所示,由平衡条件得
对玻璃管
|
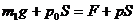
对水银柱
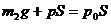
式中的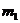 、
、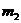 分别为玻璃管和水银柱的质量,
分别为玻璃管和水银柱的质量,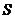 为水银柱的横截面积,解以上两式,得
为水银柱的横截面积,解以上两式,得

由牛顿第三定律可知,玻璃管对弹簧秤的拉力大小,即弹簧秤的示数为
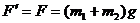
故,答案为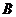 。
。
知识链接及误点警示:
①本题涉及气体压强的概念问题,压强、体积和温度是气体的三个状态参量。对于一定质量的气体来说,三个参量都不变,则这一定质量的气体就处于一定的状态中;三个参量同时变或其中的两个发生变化时,我们就说气体的状态改变了。注意,不存在只有一个参量发生变化的情况。
②这是一道受力分析、平衡条件应用的题目,平衡条件的应用应该是没有什么问题,只要受力分析正确,列出方程求解就可以了。关键在于受力分析时,特别是对于玻璃管的受力分析,容易把玻璃管上端所受的大气压力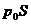 漏掉,在做类似的题目时应特别注意这一点。
漏掉,在做类似的题目时应特别注意这一点。
考点2. 气体的状态 实验定律的应用
剖析:
应用气体实验定律求解气体状态变化中的问题
1.关键是确定气体的几个不同状态,对各个状态的状态参量进行分析,准确表示出各个状态的状态参量:TVP。
(1)气体温度T。是热力学温度,分析时要注意:绝热、热的良导体、恒温箱(装置)等字眼,准确判断其温度值。
(2)气体的体积V,分析时要注意:液体的不可压缩性与固体总长的不变性。
(3)气体的压强P。三个参量中,P的分析内容最丰富,也是力、热综合的渗透点,分析压强紧紧抓住两个基本模型--活塞模型、汽缸模型进行分析,一般根据问题的需要,灵活选择,运用平衡条件或牛顿第二定律求解。
(六)、理想气体的内能及变化
1.理想气体的内能
由于理想气体分子间无相互作用力,因此不存在分子势能。所以,理想气体的内能只是气体分子热运动的分子功能总和,只与温度和分子数有关而与体积无关。
2.理想气体的内能变化
①等温变化
一定质量的理想气体在温度不变的情况下发生膨胀,由于温度保持不变,所以气体内能不变,即ΔE=0,气体膨胀对外做功,故W为负值,由W+Q=ΔE可知Q应为正值,且W与Q的绝对值相等,由此可知,在等温膨胀过程中,气体要从外界吸热,而全部用于对外做功,其系统内能不变。
②等容变化
在体积不变的情况下,对一定质量的理想气体加热,使它的温度升高,压强增大,所以内能增加,即ΔE>0。由于气体未变,外界与气体间不做功,即W=0由W+Q=ΔE知Q=ΔE。由此可知,在等容变化过程中,气体吸收的热量全部用于其内能的增加。如果气体对外放热,就只能以减少气体的内能为代价。
③等压变化
在压强不变的情况下,一定质量的理想气体,温度升高,体积增大。所以内能增加,即ΔE>0。气体对外做功,即W<0,由W+Q=ΔE>0可知,这时气体应从外界吸收热量且Q的绝对值大于W的绝对值,由此可知,在等压膨胀过程中,气体从外界吸收的热量一部分用于增加气体的内能,一部分用于对外做功。
④绝热变化
物体在状态变化过程中,如果没有与外界发生热交换,这种变化就叫绝热变化。其特点是Q=0。因此,在绝热压缩的过程中,外界对气体所做的功,全部用于增加气体的内能,使气体的温度升高。在绝热膨胀过程中,气体对外界做功,完全靠气体内能的减少,因而气体的 温度降低。
(五)、气体实验定律的微观解释:
1.气体压强的微观解释:气体分子与器壁碰撞时对器壁产生瞬时冲量,大量分子对器壁的频繁碰撞则对器壁产生______的压力,_________________即为压强。由此可见,气体的压强是大量的气体分子频繁的碰撞器壁的结果。
2.气体实验定律的微观解释
①玻意耳--马略特定律的微观解释
一定质量的气体,温度不变,即分子的总数和分子的平均速率保持不变。当气体体积减小到原来的几分子一,则单位体积内的分子数就增大到原来的几倍,气体的压强就增大到几倍。体积增大时,情况恰好相反,结果是一定质量的气体当温度一定时,气体的压强与体积成反比。
②查理定律的微观解释
一定质量的气体,体积保持不变而温度升高时,分子的平均速率增大,因而气体的压强增大。温度降低时,情况恰好相反。
③盖·吕萨克定律的微观解释
一定质量的气体,温度升高时,气体分子的平均速率增大,对器壁的碰撞次数增多,则压强增大。要保持压强不变,只有减少单位体积内的分子数,即增大气体的体积,使压强有减小的趋势。当体积增大到一定程度时,压强增大和减小的两种趋势相抵消,则能保持压强不变。
(四)、理想气体状态方程:
1.理想气体:宏观上严格遵守气体__________的气体。
2.理想气体状态方程:对一定质量的理想气体有________或_________
3.克拉珀珑方程:对给定状态下的理想气体,P、V、T遵循下列规律__________式中P、V、T为确定状态下气体的压强、体积、温度,m为气体质量,M为摩尔质量,R为摩尔恒量R=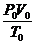 式中Po=1.013×105Pa,Vo=22.4×10-3m3To=273K。即R=8.31J/mol.k。
式中Po=1.013×105Pa,Vo=22.4×10-3m3To=273K。即R=8.31J/mol.k。
(三)、气体实验定律:
1.玻意耳定律:对一定质量的理想气体在T一定时有_________或_________。
2.查理定律:对一定质量的气体在V一定时有:_________ (Po为0℃时气体的压强)或___________、_____________。
3.盖·吕萨克定律,对一定质量的理想气体在P一定时有__________________ (Vo的气体0℃时的体积)或______;___________
(二)、气体状态参量:
1.体积V:____________。由于气体分子间的平均距离是分子直径的10倍以上,分子间的相互作用力可以认为是零,因而极易流动和扩散,总是要充满整个容器,故气体的体积等于盛气体的容器的容积。单位m3。
2.温度T(t):
(1)温度:从宏观上看,表示物体的_________;从微观上看,是物体内大量分子___________的标志,它反映了气体分子无规则的激烈程度。
(2)温标:指温度的________。常用温标有_________和_________两种,所对应的温度叫摄氏温度和热力学温度(绝对温度)。两种温度的区别与联系如下表:
|
|
摄氏温度 |
热力学温度 |
|
表示符号 |
t |
T |
|
单 位 |
摄氏度(℃) |
开尔文,简称开(k)是七个基本单位之一 |
|
0度的规 定 |
规定一标准大气压下;冰水混合物的温度为0℃,水的沸点为100℃ |
规定-273.15℃为绝对零度,记为0K,实际计算时零度不可达到只可无限接近,是低温的极限 |
|
1度的划 分 |
将水的冰点0℃和沸点100℃之间划分成100等份,每1等份叫1℃ |
将水的冰点273.15K和沸点373.15K之间划分成100等份,每1等份叫1K |
|
联 系 |
T=273+t t=T-273 △T=△t |
3.压强P:定义P=F/S。气体压强是______________________的结果,单位Pa。大量气体频繁碰撞器壁的结果。气体分子的平均速率越大,碰撞的频繁程度就越大,碰撞的作用力就越大;气体分子的密度越大,碰撞的频繁程度也越大,所以气体的压强与气体分子热运动的剧烈程度有关,也就是与气体的温度有关,同时还与单位体积中分子的数目有关,对一定质量的气体来说压强与气体的体积有关。
(一)、气体分子运动的特点
1.分子间的距离较大:气体很容易压缩,说明气体分子的间距_______。气体分子的平均间距的数量级为10-9m是分子直径数量级10-10m的10倍,故分子间的作用力十分微弱。
2.分子间的碰撞频繁:在标准状态下,1立方厘米气体中含有2.7×1019个分子。大量分子__________运动,分子间不断地发生碰撞。在标准状态下,一个空气分子在1 秒内与其它空气分子的碰撞竟达65亿次之多。故分子间的碰撞频繁。通常假定分子之间或分子与器壁之间的碰撞为完全弹性碰撞。
3.分子沿各方向运动的机会_______:由于大量分子作无规则的热运动,在某一时刻向任一方向运动的分子都有,就某一个分子在某一时刻,它向哪一方向运动,完全是偶然的。因此,在任一时刻分子沿各方向运动的机会是均等的。
4.分子速率按一定规律分布:大量分子做无规则热运动,速率有大、有小。但分子的速率却按照一定的规律分布。即“_____________”的正态分布规律。当气体温度升高时,速率大的分子数增加,分子平均速率增大,因此,温度越高,分子的热运动越___________。
|
考试大纲 |
考纲解读 |
|
1.气体实验定律
I 2.理想气体 I 3.理想气体 I |
1.理解三个气体实验定律,能结合分子运动论相关内容从微观解释这三个定律,并能用这三个定律解释问题和进行简单的定量计算,没有必要做那些难度很大的计算题。 2.要重视气体实验定律的定量计算及图象类的题。 |
8.(2010·南京模拟)17世纪英国物理学家胡克发现:在弹性限度内,弹簧的形变量与弹力成正比,这就是著名的胡克定律.受此启发,一学习小组同学研究“金属线材伸长量与拉力的关系”的探究过程如下:
A.有同学认为:横截面为圆形的金属丝或金属杆在弹性限度内,其伸长量与拉力成正比,与截面半径成反比.
B.他们准备选用一些 “由同种材料制成的不同长度、不同半径的线材”作为研究对象,用测距仪、传感器等仪器测量线材的伸长量随拉力变化的规律,以验证假设.
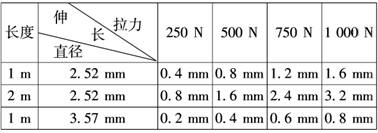 C.通过实验取得如下数据:
C.通过实验取得如下数据:
D.同学们对实验数据进行分析、归纳后,对他们的假设进行了补充完善.
(1)上述科学探究活动中,属于“制定计划”和“搜集证据”的环节分别是 、 .
(2)请根据上述过程分析他们的假设是否全部正确?若有错误或不足,请给予修正.
解析:确定研究对象,选取实验器材属“制定计划”;实验过程和测量数据属“搜集证据”.研究伸长量x与拉力F、长度L、直径D的关系时,采用控制变量法,比如长度、直径不变,再研究伸长量与力的关系,这种方法称为控制变量法.这是物理实验中的一个重要研究方法.
答案:(1)B C (2)他们的假设不是全部正确.在弹性限度内,金属丝(杆)的伸长量与拉力成正比,与截面半径的平方成反比,还与金属丝(杆)的长度成正比
()
4.000 mm,那么测量工具a应该是 ,测量工 图实-3-14
具b应该是 .
(3)下面的表格是橡皮筋受到的拉力F与伸长量x的实验记录.

请作出F-x图象,由图象可求得该橡皮筋的劲度系数k= N/m.
(4)这种橡皮筋的Y值等于 .
解析:(1)在弹性限度内,弹力F与伸长量x成正比,F=kx,又根据题意可知,k=YS/L.
则F=kx=Y·x
得出杨氏模量Y=
各物理量取国际单位得杨氏模量的单位是N/m2=Pa,选项D正确.
(2)根据精确度判断可知a为毫米刻度尺,b为螺旋测微器.
(3)根据表格数据,描点、连线,可得F-x图象如图所示.根据斜率的物量意义表示劲度系数k,
k=≈3.1×102 N/m.
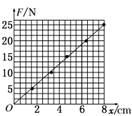
(4)根据Y=kL/S求得,Y≈5×106 Pa.
答案:(1)D (2)毫米刻度尺 螺旋测微器 (3)图象见解析图 3.1×102 (4)5×106 Pa
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com