
1.设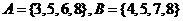 ,求
,求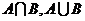 .
.
1.1.3集合的基本运算
练习(第11页)
3.解:(1)因为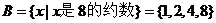 ,所以
,所以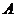
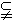
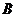 ;
;
(2)当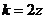 时,
时,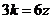 ;当
;当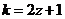 时,
时,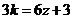 ,
,
即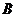 是
是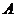 的真子集,
的真子集,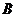
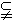
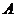 ;
;
(3)因为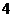 与
与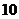 的最小公倍数是
的最小公倍数是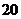 ,所以
,所以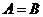 .
.
3.判断下列两个集合之间的关系:
(1)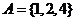 ,
,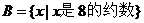 ;
;
(2) ,
,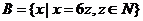 ;
;
(3)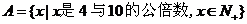 ,
,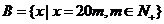 .
.
2.(1)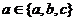
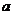 是集合
是集合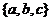 中的一个元素;
中的一个元素;
(2)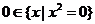
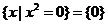 ;
;
(3)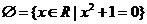 方程
方程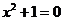 无实数根,
无实数根, ;
;
(4)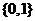
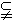
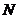 (或
(或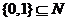 )
) 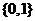 是自然数集合
是自然数集合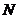 的子集,也是真子集;
的子集,也是真子集;
(5)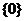
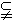
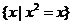 (或
(或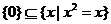 )
) 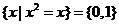 ;
;
(6) 方程
方程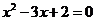 两根为
两根为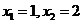 .
.
2.用适当的符号填空:
(1)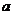 ______
______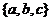 ;
(2)
;
(2)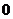 ______
______ ;
;
(3)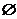 ______
______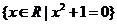 ; (4)
; (4)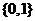 ______
______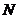 ;
;
(5)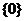 ______
______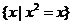 ;
(6)
;
(6)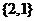 ______
______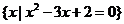 .
.
1.解:按子集元素个数来分类,不取任何元素,得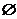 ;
;
取一个元素,得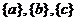 ;
;
取两个元素,得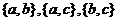 ;
;
取三个元素,得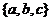 ,
,
即集合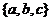 的所有子集为
的所有子集为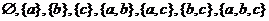 .
.
1.写出集合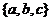 的所有子集.
的所有子集.
1.1.2集合间的基本关系
练习(第7页)
2.解:(1)因为方程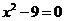 的实数根为
的实数根为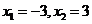 ,
,
所以由方程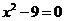 的所有实数根组成的集合为
的所有实数根组成的集合为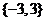 ;
;
(2)因为小于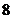 的素数为
的素数为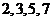 ,
,
所以由小于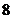 的所有素数组成的集合为
的所有素数组成的集合为 ;
;
(3)由 ,得
,得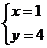 ,
,
即一次函数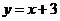 与
与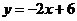 的图象的交点为
的图象的交点为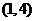 ,
,
所以一次函数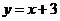 与
与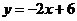 的图象的交点组成的集合为
的图象的交点组成的集合为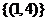 ;
;
(4)由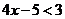 ,得
,得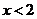 ,
,
所以不等式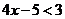 的解集为
的解集为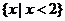 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com