
(17)(本小题满分10分)当n∈N*时,证明:
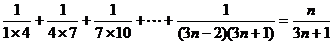
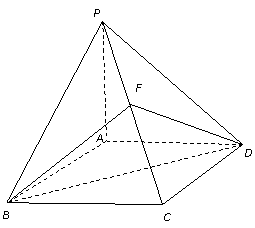
(18)( 本小题满分12分)如图,已知四棱锥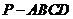 的底面
的底面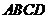 是菱形,
是菱形,
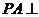 平面
平面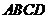 , 点
, 点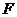 为
为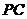 的中点.
的中点.
(1)求证 :
: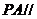 平面
平面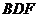 ;
;
(2)求证: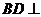 平面
平面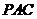 ;
;
(3)若PA=AB=2,∠ABC= 60o,求二面角P-BC-A的大小。
60o,求二面角P-BC-A的大小。
(19)(本小题满分12分)设函数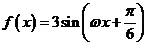 ,
,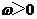 ,
,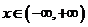 ,且以
,且以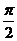 为最小正周期.
为最小正周期.
(1)求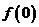 ;
;
(2)求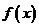 的解析式;
的解析式;
(3)已知 ,求
,求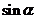 的值.
的值.
(20)(本小题满分12分)设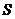 是不等式
是不等式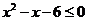 的解集,整数
的解集,整数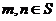 。
。
(1)记使得“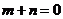 成立的有序数组
成立的有序数组 ”为事件A,试列举A包含的基本事件;
”为事件A,试列举A包含的基本事件;
(2)设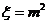 ,求
,求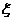 的分布列及其数学期望
的分布列及其数学期望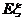 。
。
(21)(本小题满分12分)已知等差数列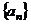 满足:
满足: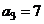 ,
,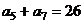 ,
,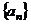 的前
的前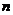 项和为
项和为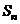
(Ⅰ) 求
求 及
及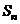 ;
;
(Ⅱ)令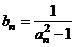 (
(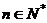 ),求数列
),求数列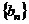 的前
的前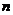 项和为
项和为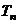
(22)(本小题满分12分)已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线 ,使得直线
,使得直线 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与 的距离等于4?若存在,求出
的距离等于4?若存在,求出 直线
直线 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
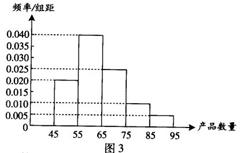 (13)为了调查某厂工人生产某种产品的能力,随机抽查 了20位工人某天生产该产品的数量.产品数量的分组区间为
(13)为了调查某厂工人生产某种产品的能力,随机抽查 了20位工人某天生产该产品的数量.产品数量的分组区间为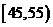 ,
,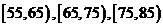 ,
,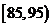 由此得到频率分布直方图如图3,则这20名工人中一天生产该产品数量在
由此得到频率分布直方图如图3,则这20名工人中一天生产该产品数量在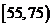 的人数是 .
的人数是 .
(14)若随机变量 ,则
,则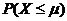 =________.
=________.
(15)已知a,b,c分别是△ABC的三个内角A, B,C所对的边,若a=1,b=
B,C所对的边,若a=1,b=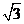 ,A+C=2B,则sinA=
.
,A+C=2B,则sinA=
.
(16)已知圆C过点(1,0),且圆心在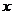 轴的正半轴上,直线
轴的正半轴上,直线 :
: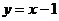 被该圆所截得的弦长为
被该圆所截得的弦长为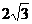 ,则圆C的标准方程为____________________。
,则圆C的标准方程为____________________。
A.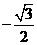 B.
B.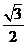 C.-
C.-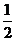 D.
D.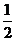
(2)设全集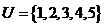 ,集合
,集合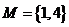 ,
,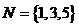 ,则
,则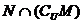 =
=
A.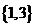 B.
B.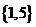 C.
C.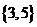 D.
D.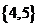
(3)若变量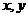 满足约束条件
满足约束条件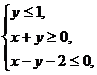 则
则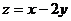 的最大值为
的最大值为
A.4 B.3 C.2 D.1
(4)已知各项均为正数的等比数列{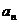 },
},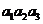 =5,
=5,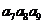 =10,则
=10,则
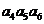 =
=
A.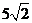 B.7 C.6
B.7 C.6  D.
D.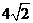
(5)双曲线方程为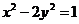 ,则它的右焦点坐标为
,则它的右焦点坐标为
A.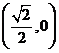 B.
B.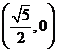 C.
C. D.
D.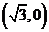
(6)已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.6826,则P(X>4)=
A.0.1588 B.0.1587 C.0.1586 D.0.1585
(7)设向量 ,
,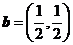 ,则下列结论中正确的是
,则下列结论中正确的是
A.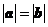 B.
B.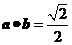
C.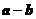 与
与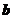 垂直 D.
垂直 D.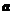 ∥
∥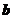
(8)若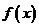 是
是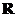 上周期为5的奇函数,且满足
上周期为5的奇函数,且满足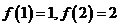 ,则
,则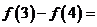
A.-1 B.1 C.-2 D.2
(9)某校开设A类选修课3门,B类选择课4门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有
A.30种 B.35种 C.42种 D.48种
(10)直三棱柱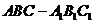 中
中 ,若
,若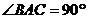 ,
,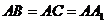 ,则异面直线
,则异面直线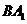 与
与 所成的角等于
所成的角等于
A.30° B.45° C.60° D.90°
(11)已知抛物线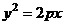 (
(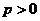 ),过其焦点且斜率为1的直线交抛物线于A、B两点,若线段AB的中点的纵坐标为2,则该抛物线的准线方程为
),过其焦点且斜率为1的直线交抛物线于A、B两点,若线段AB的中点的纵坐标为2,则该抛物线的准线方程为
A. 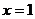 B.
B.
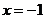 C.
C. 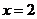 D.
D. 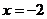
(12)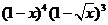 的展开式
的展开式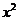 的系数为
的系数为
A. 3 B.-3 C.0 D.-6
第Ⅱ卷 (非选择题共 90分)
(17)(本小题满分10分)如图,已知四棱锥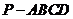 的底面
的底面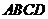 是菱形,
是菱形,
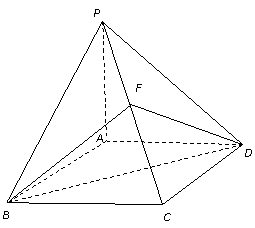
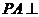 平面
平面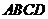 , 点
, 点 为
为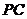 的中点.
的中点.
(Ⅰ)求证: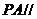 平面
平面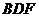 ;
;
(Ⅱ)求证: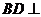 平面
平面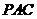 .
.
(18)(本小题满分12分)设函数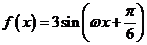 ,
,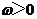 ,
,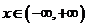 ,且以
,且以 为最小正周期.
为最小正周期.
(1)求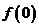 ;
;
(2)求
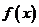 的解析式;
的解析式;
(3)已知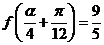 ,求
,求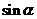 的
的 值.
值.
(19)(本小题满分12分)甲、乙两人各进行3次射击,甲每次击中目标的概率为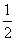 ,乙每次击中目标的概率为
,乙每次击中目标的概率为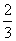 ,
,
(1)求乙至多击中目标2次的概率;
(2)求甲恰好比乙多击中目标2次的概率.
(20)(本小题满分12分)已知等差数列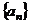 满足:
满足: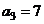 ,
,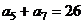 ,
,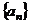 的前
的前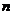 项和为
项和为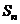
(Ⅰ)求 及
及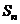 ;
;
(Ⅱ)令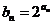 (
(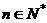 ),求数列
),求数列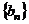 的前
的前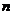 项和为
项和为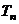
(21)(本小题满分12分)已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线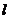 ,使得直线
,使得直线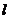 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与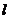 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线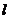 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
(22)( 本小题满分12分)设函数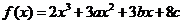 在
在 及
及 时取得极值.
时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的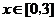 ,都有
,都有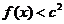 成立,求c的取值范围.
成立,求c的取值范围.
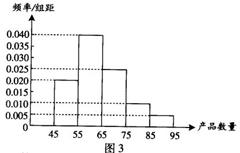 (13)为了调查某厂工人生产某种产品的能力,随机抽查 了20位工人某天生产该产品的数量.产品数量的分组区间为
(13)为了调查某厂工人生产某种产品的能力,随机抽查 了20位工人某天生产该产品的数量.产品数量的分组区间为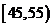 ,
,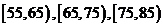 ,
,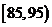 由此得到频率分布直方图如图3,则这20名工人中一天生产该产品数量在
由此得到频率分布直方图如图3,则这20名工人中一天生产该产品数量在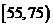 的人数是 .
的人数是 .
(14)曲线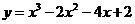 在点
在点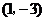 处的切线方程是 .
处的切线方程是 .
(15)已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=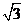 ,A+C=2B,则sinA=
.
,A+C=2B,则sinA=
.
(16)已知圆C过点(1,0),且圆心在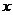 轴的正半轴上,直线
轴的正半轴上,直线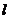 :
: 被该圆所截得的弦长为
被该圆所截得的弦长为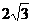 ,则圆C的标准方程为____________________。
,则圆C的标准方程为____________________。
A.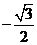 B.
B.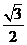 C.-
C.-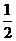 D.
D.
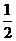
(2)设全集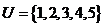 ,集合
,集合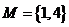 ,
,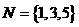 ,则
,则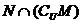 =
=
A.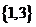 B.
B.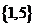 C.
C.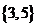 D.
D.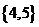
(3)若变量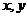 满足约束条件
满足约束条件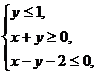 则
则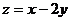 的最大值为
的最大值为
A.4 B.3 C.2 D.1
(4)已知各项均为正数的等比数列{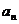 },
},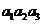 =5,
=5,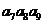 =10,则
=10,则
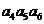 =
=
A.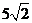 B.7 C.6
D.
B.7 C.6
D.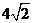
(5)双曲线方程为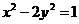 ,则它的右焦点坐标为
,则它的右焦点坐标为
A.
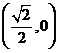 B.
B.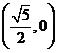 C.
C.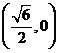 D.
D.
(6)某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况, 现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
(A)9 (B)18 (C)27 (D) 36
(7)设向量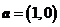 ,
,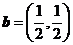 ,则下列结论中正确的是
,则下列结论中正确的是
A.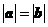 B.
B.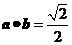
C.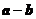 与
与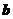 垂直 D.
垂直 D.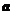 ∥
∥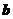
(8)若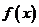 是
是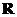 上周期为5的奇函数,且满足
上周期为5的奇函数,且满足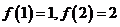 ,则
,则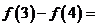
A.-1 B. 1 C.-2 D.2
1 C.-2 D.2
(9)函数f(x)=x4-2x2+6的单调递增区间是
 ( )
( )
A.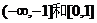 B.
B.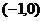 C.(-1,0)和(1,+∞) D.(0,1)
C.(-1,0)和(1,+∞) D.(0,1)
(10) 直三
直三 棱柱
棱柱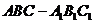 中,若
中,若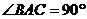 ,
,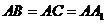 ,则异面直线
,则异面直线 与
与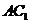 所成的角等于
所成的角等于
A.30° B.45° C.60° D.90°
(11)已知抛物线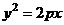 (
(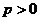 ),过其焦点且斜率为1的直线交抛物线于A、B两点,若线段AB的中点的纵坐标为2,则该抛物线的准线方程为
),过其焦点且斜率为1的直线交抛物线于A、B两点,若线段AB的中点的纵坐标为2,则该抛物线的准线方程为
(A)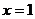 (B)
(B)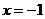
(C)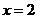 (D)
(D)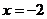
(12)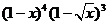 的展开式
的展开式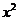 的系数为
的系数为
A.3 B.-3 C.0 D.-6
第Ⅱ卷 (非选择题共 90分)
32.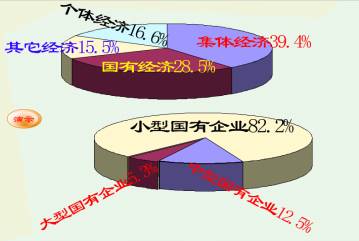
我国发展社会主义市场经济,必须坚持公有制为主体,但决不是要搞纯而又纯的公有制。新中国成立以来经济发展正反两方面的经验已经证明:搞纯而又纯的公有制,不仅不能促进反而会阻碍生产力的发展。
马克思主义认为:任何一个社会的基本经济制度都不可能通过道义原则或信仰原则来确立,人们也不可能仅凭主观意愿来设计基本经济制度。
(1)上述图片经济现象说明了什么?(5分)
(2)请你依据材料中马克思的论述,说明我国现阶段的基本经济制度应该依据什么来确立的?(5分)
(3)“纯而又纯的公有制”有哪些具体内容?我国现阶段为什么不能“搞纯而又纯的公有制”?(10分)
2010年8月月考政治题《经济常识》第一单元 基本经济理论
31.所谓3G,其全称为3rd Generation,指第三代数字通信。1995年问世的第一代数字手机只能进行语音通话;1996到1997年出现的第二代数字手机便增加了接收数据的功能;第三代与前两代的主要区别是它能够处理图像、音乐、视频流等多种媒体形式,提供包括网页浏览、电话会议、电子商务等多种信息服务。
从2009年初我国宣布进入3G时代开始,中国接近7亿的手机用户已陆续迎来“与网随行”的日子,视频通话、电视直播,这些等待已久的画面都将成为现实生活的一部分。买一部3G手机,实现视频通话和宽带上网,成为很多时尚达人和“白骨精(白领、骨干、精英)一族”的超级首选。但要把这种使用欲望转化为购买行动,还需要一段时间。因为“物以稀为贵”,目前3G消费价格较高。
(1)一种新的电子产品刚出现时往往价格较高,但一段时间后则价格下降而成为大众消费产品,这其中的原因是什么?(5分)
(2)目前3G消费的价格高,是否意味着不等价交换?(5分)
(3)由2G手机到3G手机,消费者更关注的是什么?对生产者有什么启示?(10分)
运用所学知识对下面的问题进行分析说明。
30.《企业破产法》规定:“破产企业的法定代表人和破产企业的上级主管部门的领导人,因玩忽职守造成企业破产,致使国 家财产遭受重大损失的,依照《中华人民共和国刑法》第一百八十七条的规定追究刑事责任。”这表明
家财产遭受重大损失的,依照《中华人民共和国刑法》第一百八十七条的规定追究刑事责任。”这表明
①政府的宏观调控要置于法律规范之下 ②企业的经济活动必须依法进行 ③市场主体的生产经营活动受法律制约 ④市场秩序的 建立需要法律的维护
建立需要法律的维护
A.①②③ B.①③④ C.①②④ D.②③④
29.
漫画“如此打折”给我们的启示是
A.坚持公平与效率的辩证统一 B.要关注社会公平
C.防止收入分配差距过分扩大 D.为了效率关注公平
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com