17．(本小题满分5分)

解：∵ 一次函数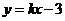的图象经过点，

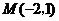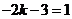∴ ．············································································································ 1分

解得 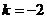．··············································································································· 2分

∴ 此一次函数的解析式为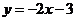．········································································ 3分

令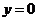，可得．

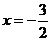∴ 一次函数的图象与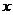轴的交点坐标为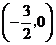．························································ 4分

令，可得．

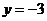∴ 一次函数的图象与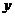轴的交点坐标为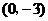．·························································· 5分

16．(本小题满分5分)

证明：在正方形ABCD中，

知AB=AD=DC=BC，∠B=∠D=90^O．-------------------------------------------------2分

∵　 AE=AF，

∴　 AB-AE=AD-AF．

即　 BE=DF．·················································································································· 3分

在△BCE和△DCF中，

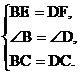
∴　 △BCE≌△DCF．····································································································· 4分

∴　 CE＝CF．················································································································ 5分

15．(本小题满分5分)

解：原式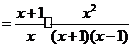······················································································· 3分

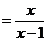　　　　　　 ．·········································································································· 5分

14．(本小题满分5分)

解：去括号，得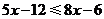．················································································ 1分

移项，得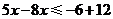．························································································ 2分

合并，得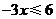．······································································································ 3分

系数化为1，得．································································································ 4分

不等式的解集在数轴上表示如图：

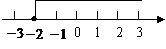
······································································································································ 5分

13．(本小题满分5分)

解：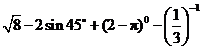

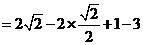·································································································· 4分

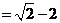．··················································································································· 5分

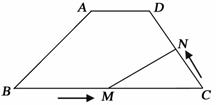
25．如图，在梯形ABCD中，AD∥BC，AD＝3，CD＝5，BC＝10，梯形的高为4．动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动；动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动．设运动的时间为t(秒)．

(1)当MN∥AB时，求t的值；

(2)试探究：t为何值时，△CMN为等腰三角形．

2010年密云县初中毕业考试

数学试卷答案参考及评分标准

24．如图，将腰长为的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限，其中点A在y轴上，点B在抛物线y＝ax²+ax－2上，点C的坐标为(－1，0)．

(1)点A的坐标为　　　　 ，点B的坐标为　　　　 ；

(2)抛物线的关系式为　　　　　　　　　　　 ，其顶点坐标为　　　　　　 ；

(3)将三角板ABC绕顶点A逆时针方向旋转90°，到达的位置．请判断点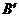、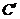是否在(2)中的抛物线上，并说明理由．

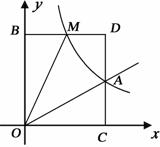
23．已知：如图，正比例函数y＝ax的图象与反比例函数y＝的图象交于点A(3，2)．

(1)试确定上述正比例函数和反比例函数的表达式；

(2)根据图象回答，在第一象限内，当x取何值时，反比例函数的值大于正比例函数的值？

(3)M(m，n)是反比例函数图象上的一动点，其中0＜m＜3过点M作直线MB∥x轴，交y轴于点B；过点A作直线AC∥y轴交x轴于点C，交直线MB于点D．当四边形OADM的面积为6时，请判断线段BM与DM的大小关系，并说明理由．

22．(1)观察与发现：

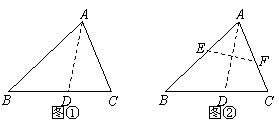在一次数学课堂上，老师把三角形纸片ABC(AB＞AC)沿过A点的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片(如图①)；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF(如图②)．有同学说此时的△AEF是等腰三角形，你同意吗？请说明理由．

(2)实践与运用

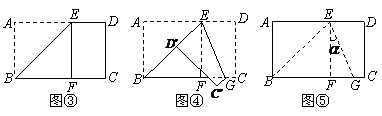将矩形纸片ABCD沿过点B的直线折叠，使点A落在BC边上的点F处，折痕为BE(如图③)；再沿过点E的直线折叠，使点D落在BE上的点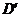处，折痕为EG(如图④)；再展平纸片(如图⑤)．试问：图⑤中∠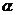的大小是多少？(直接回答，不用说明理由)．

21．为了比较市场上甲、乙两种电子钟每日走时误差的情况，从这两种电子钟中，各随机抽取10台进行测试，两种电子钟走时误差的数据如下表(单位：秒)：

(1)计算甲、乙两种电子钟走时误差的平均数；

(2)计算甲、乙两种电子钟走时误差的方差；

(3)根据经验，走时稳定性较好的电子钟质量更优．若两种类型的电子钟价格相同，请问：你用哪种电子钟？为什么？