3．匀速圆周运动、描述匀速圆周运动的物理量、匀速圆周运动的实例分析。

正确理解并掌握匀速圆周运动、线速度、角速度、周期和频率、向心加速度、向心力的概念及物理意义，并掌握相关公式。

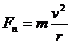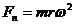圆周运动与其他知识结合时，关键找出向心力，再利用向心力公式 或列式求解。向心力可以由某一个力提供，也可由某一个力的分力提供，还可以由合外力提供，在匀速圆周运动中，向心力指向圆心，其大小不变，作用是改变线速度的方向，不改变线速度的大小；在变速圆周运动中，物体所受的合外力不一定指向圆心，各力沿半径的分量的合力指向圆心，此合力提供向心力，大小、方向均变化；与半径垂直的各分力的合力改变速度大小，此合力产生切向加速度，在中学阶段不做研究。

对匀速圆周运动的实例分析应结合受力分析，找准圆心位置，结合牛顿第二定律和向心力公式列方程求解，要注意绳类的约束条件为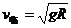，杆类的约束条件为。

l、曲线运动和运动的合成与分解

物体的运动轨迹不是直线的运动称为曲线运动，曲线运动的条件可从两个角度来理解：①从运动学角度来理解：物体的加速度方向与速度方向不在同一条直线上；②从动力学角度来理解：物体所受合力的方向与物体的速度方向不在同一条直线上。曲线运动的速度方向沿曲线的切线方向，曲线运动是一种变速运动。

曲线运动是一种复杂的运动，为了简化解题过程引入了运动的合成和分解。一个复杂的运动可根据运动的实际效果按正交分解或按平行四边形定则进行分解。合运动与分运动是等效替代关系，它们具有独立性和等时性的特点。运动的合成是运动分解的逆运算，同样遵循平行四边形定则。

2、平抛运动

平抛运动具有水平初速度且只受重力作用，是匀变速曲线运动。研究平抛运动的方法是利用运动的合成与分解，将复杂运动分解成水平方向的匀速直线运动和竖直方向的自由落体运动。其运动规律为：①水平方向：a_x=0，v_x=v₀，x=v₀t；②竖直方向：a_y=g，v_y=gt，y=gt²/2；

③合运动：a=g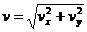，，v与 v₀的夹角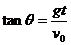

平抛运动中飞行时间仅由抛出点与落地点间的竖直高度决定，即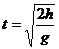与v₀无关。水平射程x=v₀。

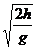2、基本解题方法

(1)如何运用运动的分解与合成方法来研究曲线运动呢？

①利用运动的合成与分解研究曲线运动的思维流程：

②在处理实际问题中应注意：

ⅰ 只有深刻挖掘曲线运动的实际运动效果，才能明确曲线运动应分解为哪两个方向上的直线运动。这是分析处理曲线运动的出发点。

ⅱ 进行等效合成时，要寻找两分运动时间的联系--等时性。这往往是分析处理曲线运动问题的切人点。

(2)处理匀速圆周运动问题的解题思路。

所有匀速圆周运动的有关命题，重点都是对牛顿第二定律F=ma在曲线运动中具体应用的考查。通常的解题思路为：首先分析向心力的来源，然后确定物体圆周运动轨道平面、圆心、圆半径，写出与向心力所对应的向心加速度表达式，同时，力求将题目的待求量如：未知力、未知线速度、未知周期等包含到向心力或向心加速度的表达式中，最后，依据F=ma列方程求解。

1、物理思维方法

本章中，我们借助运动的分解与合成方法，研究了曲线运动的规律，达到了“曲径通幽”的效果，贯穿着物理学上的等效思维方法，值得体会。

等效方法不但能使问题化繁为简，化难为易，而且能加深我们对物理概念和规律的认识，强化思维，丰富想象，培养我们独立获取知识的能力。

本章我们学习了物体做曲线运动的条件以及运动的合成和分解，并研究了两种曲线运动：平抛运动和匀速圆周运动。运动的合成和分解是研究曲线运动的基本方法，本章的知识框图如下：

第一节　 短文改错(满分10分)

　　　　 下面短文中有10处错误。请在有错误的地方增加，删除或修改某个单词。

　　　　 增加：在缺词处加一个漏词符号(∧)，并在其下面写上该加的词。

　　　　 删除：把多余的词用斜线(﹨)划掉。

　　　　 修改：在错的词下划一横线，并在该词下面写上修改后的词。

　　　　 注意：1，每处错误及其修改均仅限一词。

　　　　　　　 2，只允许修改10处，多者(从第11处起)不计分。

　As the working hours becoming shorter and shorter and holidays becoming longer and longer, what to spend the leisure time had become a hot topic. The use of free time discloses many about one's values, interests and so on. Some might be interesting in movies and television. Some enjoy sports. Others are like parties or traveling. Obvious, the use of free time is a good means of relaxation. It’s benefits go beyond this. What people do in leisure hours enables them satisfy their wishes. This can contribute to intellectual growth and promote social activities as well as.