
7. 如图,在正方体中,二面角的余弦值是( )
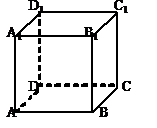 A. B.
A. B.
C. D.
6. 已知直线l,m,平面和,且,给出下列三个命题
①若,则;②若,则;③若,则。其中正确命题的个数是( )
A. 0个 B. 1个 C. 2个 D. 3个
5.以下命题正确的是 ( )
A.α,β都是第一象限角,若cosα>cos β,则sinα>sinβ
B.α, β都是第二象限角,若sinα>sin β,则tgα>tgβ
C.α,β都是第三象限角,若cosα>cosβ,则sinα>sinβ
D.α,β都是第四象限角,若sinα>sinβ,则tgα>tgβ
4.夹在两个平行平面之间的球、圆柱、圆锥在这两个平面上的射影都是等圆,则它们的体积之比为( )
A.2:3:1 B.3:2:1 C.3:6:2 D.6:8:3
3.极坐标系中,点A(1,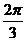 )到圆
)到圆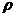 =2cos
=2cos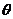 上动点的距离的最大值为 ( )
上动点的距离的最大值为 ( )
A.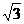 -1 B.
-1 B.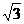 +1 C.2 D.1
+1 C.2 D.1
2.函数y=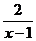 的定义域是(-
的定义域是(-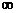 ,1)
,1)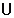 [2,5),则其值域是 ( )
[2,5),则其值域是 ( )
A.(-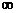 ,0)
,0)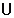 (
( 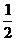 ,2] B.(-
,2] B.(-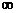 ,2]
,2]
C.(-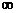 ,
,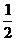 )
)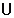 [2,+
[2,+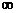 ) D.(0,+
) D.(0,+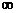 )
)
只有一项是符合题目要求的。
1.已知集合A={x|a-1≤x≤a+2},B={x| 3<x<5},则能使A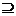 B成立的实数a的取值范围是 ( )
B成立的实数a的取值范围是 ( )
A.{a|3<a≤4} B.{a|3≤a≤4} C.{a|3<a<4} D.
20.(本小题满分14分)
已知函数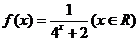 。
。
(1)证明: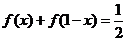
(2)若数列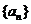 的通项公式为
的通项公式为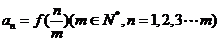 ,求数列
,求数列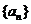 的前
的前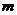 项和
项和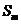 ;
; 

(3)设数列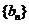 满足:
满足: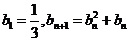 ,设
,设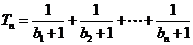 ,
,
若(2)中的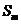 满足对任意不小于2的正整数
满足对任意不小于2的正整数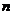 ,
,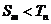 恒成立,
恒成立,
试求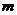 的最大值。
的最大值。
2009---2010学年度高三级第一学期第一次联考
19.(本小题满分14分)
已知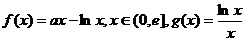 ,其中
,其中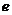 是自然常数,
是自然常数,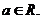
(1)讨论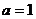 时,
时, 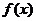 的单调性、极值;
的单调性、极值; 

(2)求证:在(1)的条件下,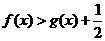 ;
;
(3)是否存在实数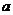 ,使
,使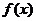 的最小值是3,若存在,求出
的最小值是3,若存在,求出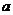 的值;若不存在,说明理由.
的值;若不存在,说明理由.
18.(本小题满分14分)已知 ,点
,点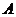 在
在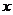 轴上,点
轴上,点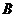 在
在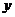 轴的正半轴,点
轴的正半轴,点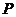 在直线
在直线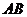 上,且满足
上,且满足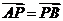 ,
,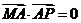 .
. 

(Ⅰ)当点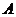 在
在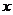 轴上移动时,求动点
轴上移动时,求动点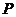 的轨迹
的轨迹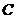 方程;
方程;
(Ⅱ)过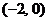 的直线
的直线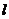 与轨迹
与轨迹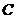 交于
交于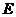 、
、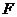 两点,又过
两点,又过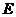 、
、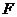 作轨迹
作轨迹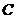 的切线
的切线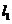 、
、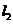 ,当
,当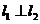 ,求直线
,求直线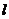 的方程.
的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com