
19.(本小题满分14分)
各项均为正数的数列{an}的前n项和Sn,函数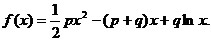
(其中p、q均为常数,且p>q>0),当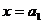 时,函数f(x)取得极小值,点
时,函数f(x)取得极小值,点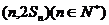 均在函数
均在函数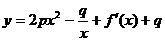 的图象上,(其中f′(x)是函数f(x)的导函数)
的图象上,(其中f′(x)是函数f(x)的导函数)
(1)求a1的值;
(2)求数列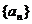 的通项公式;
的通项公式;
(3)记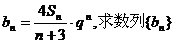 的前n项和Tn.
的前n项和Tn.
18.(本小题满分14分)
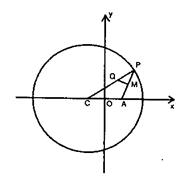 已知点C为圆
已知点C为圆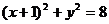 的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且
的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且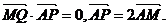
(Ⅰ)当点P在圆上运动时,求点Q的轨迹方程;
(Ⅱ)若直线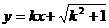 与(Ⅰ)中所求点Q
与(Ⅰ)中所求点Q
的轨迹交于不同两点F,H,O是坐标原点,
且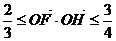 ,求△FOH的面积.
,求△FOH的面积.
17.(本小题满分14分)班主任为了对本班学生的考试成绩进行分析,决定从全班25名女同学,15名男同学中随机抽取一个容量为8的样本进行分析.
(Ⅰ)如果按性别比例分层抽样,可以得到多少个不同的样本?(只要求写出算式即可,不必计算出结果).(Ⅱ)随机抽出8位,他们的数学分数从小到大排序是:60、65、70、75、80、85、90、95,物理分数从小到大排序是:72、77、80、84、88、90、93、95.
(1)若规定85分以上(包括85分)为优秀,求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率;(2)若这8位同学的数学、物理分数对应如下表:
|
学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
数学分数x |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
|
物理分数y |
72 |
77 |
80 |
84 |
88 |
90 |
93 |
95 |
根据上表数据用变量y与x的相关系数或散点图说明物理成绩y与数学成绩x之间是否具有线性相关性?如果具有线性相关性,求y与x的线性回归方程(系数精确到0.01);如果不具有线性相关性,请说明理由.
参考公式:相关系数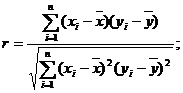 回归直线的方程是:
回归直线的方程是: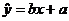 ,
,
其中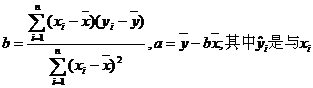 对应的回归估计值.
对应的回归估计值.
参考数据: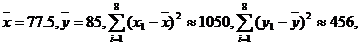
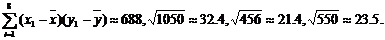
|
16.(本题满分12分)
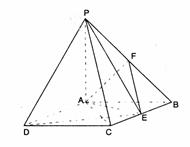 如图:四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=
如图:四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=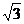 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
(Ⅰ)点E为BC的中点时,试判断EF与平面
PAC的位置关系,并说明理由;
(Ⅱ)证明:无论点E在BC边的何处,都有PE⊥AF;
(Ⅲ)当BE等于何值时,PA与平面PDE所成角的大小为45°
(本题满分12分)
15.设向量 .
.
|
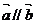 ,求
,求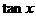 的值;
的值;
(2)求函数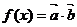 的最大值及相应x的值.
的最大值及相应x的值.
14.考察下列一组不等式: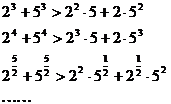 将上述不等式在左右两端视为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式为 .
将上述不等式在左右两端视为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式为 .
13.在极坐标系中,定点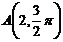 ,点B在直线
,点B在直线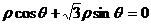 上运动,当线段AB最短时,点B的极坐标为__________.
上运动,当线段AB最短时,点B的极坐标为__________.
12.在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有: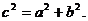
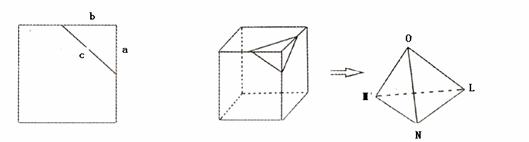
设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN,如果用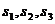 表示三个侧面面积,
表示三个侧面面积,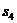 表示截面面积,那么你类比得到的结论是
.
表示截面面积,那么你类比得到的结论是
.
11.等比数列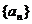 的公比为
的公比为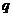 ,其前
,其前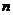 项的积为
项的积为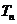 ,并且满足条件
,并且满足条件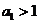 ,
,
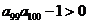 ,
,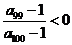 。给出下列结论:①
。给出下列结论:①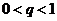 ;②
;②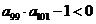 ③
③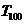 的值是
的值是
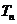 中最大的;④使
中最大的;④使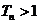 成立的最大自然数
成立的最大自然数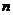 等于198。
等于198。
其中正确的结论是 .
10.对于函数y=f(x),xÎD,若存在常数c,使对任意x1ÎD,存在唯一的x2ÎD,满足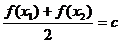 ,则称函数f(x)在D上的均值为c,现已知函数:① y=2x,② y=x5,③ y=2sinx,④ y=lgx,则满足在其定义域上均值为2的函数的序号是__________(填上所有符合要求的函数的序号)。
,则称函数f(x)在D上的均值为c,现已知函数:① y=2x,② y=x5,③ y=2sinx,④ y=lgx,则满足在其定义域上均值为2的函数的序号是__________(填上所有符合要求的函数的序号)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com