
7.
设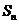 是等比数列
是等比数列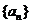 的前
的前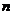 项和,若
项和,若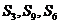 成等差数列,则
成等差数列,则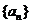 的公比
的公比 为
为
A.1 B.1或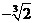 C.
C.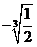 D.
D.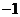 或
或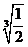
6.已知函数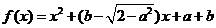 是偶函数,则此函数的图象与y轴交点的纵坐标的最大值为
是偶函数,则此函数的图象与y轴交点的纵坐标的最大值为
A.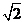 B.2
C.4
D.-2
B.2
C.4
D.-2
4.已知向量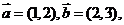 若
若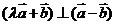 ,则
,则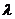 =
=
A.  B.
B.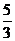 C. 0
D. -7
C. 0
D. -7
5(文).有下列四种变换方式:
①向左平移 ,再将横坐标变为原来的
,再将横坐标变为原来的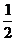 ; ②横坐标变为原来的
; ②横坐标变为原来的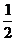 ,再向左平移
,再向左平移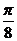 ;
;
③横坐标变为原来的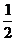 ,再向左平移
,再向左平移 ; ④向左平移
; ④向左平移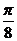 ,再将横坐标变为原来的
,再将横坐标变为原来的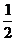 ;
;
其中能将正弦曲线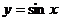 的图像变为
的图像变为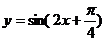 的图像的是
的图像的是
A.①③ B.①② C.②④ D.①②④
5(理).设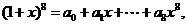 则
则 中偶数的个数为
中偶数的个数为
A.2 B.7 C.6 D.5
2.若 ,其中a、b∈R,i是虚数单位,则
,其中a、b∈R,i是虚数单位,则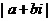 =
=
A. B.
B.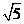 C.
C.
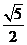 D.
D.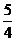
3(文).已知直线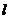 与两个不同的平面
与两个不同的平面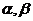 ,则下列每题正确的是
,则下列每题正确的是
A.若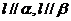 ,则
,则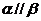 B.若
B.若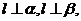 则
则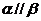
C.若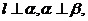 则
则 D.若
D.若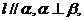 则
则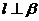
3(理).设随机变量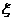 服从正态分布
服从正态分布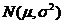 ,且函数
,且函数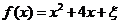 没有零点的概率为
没有零点的概率为 ,则
,则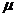 为
为
A. 1 B. 4 C. 2 D. 不能确定
1.设
 ,
,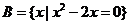 ,则
,则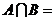
A. B.
B.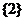 C.
C.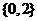 D.
D.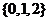
21.已知数列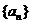 的首项
的首项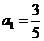 ,
,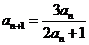 ,
, .
.
(1)求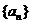 的通项公式;
的通项公式;
(2)证明:对任意的 ,
,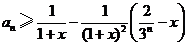 ,
, ;
;
(3)证明: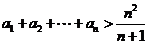 .
. 
20.如图,已知直线l: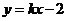 与抛物线C:
与抛物线C: 交于A,B两点,
交于A,B两点,
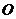 为坐标原点,
为坐标原点,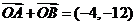 .
. 
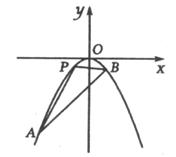 (1)求直线l和抛物线C的方程;
(1)求直线l和抛物线C的方程;
(2)抛物线上一动点P从A到B运动时,求△ABP面积最大值.
19.设函数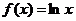 ,
,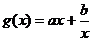 ,函数
,函数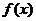 的图象与x轴的交点也在函数
的图象与x轴的交点也在函数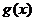
的图象上,且在此点有公切线.
(1)求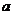 、
、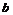 的值;
的值; 
(2)对任意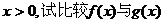 的大小.
的大小.
17. 为了了解高中学生的生长发育情况,学校抽取了高中阶段学生50人进行身高调查,根据调查结果画出频率分布直方图如图所示
为了了解高中学生的生长发育情况,学校抽取了高中阶段学生50人进行身高调查,根据调查结果画出频率分布直方图如图所示
(1)根据图中数据,求被调查的50人中身高在165到170之间的人数。
(2)(文)若在165到170之间任选一人,在170到175之间任选一人,两人身高相差超过5厘米的概率是多少? 
(2)(理)若在165到175之间任选二人,两人身高相差超过5厘米的概率是多少?

18(理).如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,
AB=BC=CE=2CD=2,∠BCE=1200,F为AE中点. 
(1)求证:平面ADE⊥平面ABE ;
(2)求二面角A-EB-D的大小的余弦值;
(3)求点F到平面BDE的距离。
18(文).如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,EC⊥BC,
AB=BC=CE=2CD=2,F为AE中点.
(1)求证:平面ADE⊥平面ABE ; 
(2)求三棱锥 的体积
的体积
16.已知:函数 .
.
(1)求函数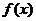 的最小正周期和值域;
的最小正周期和值域; 
(2)若函数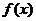 的图象过点
的图象过点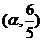 ,
,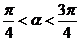 .求
.求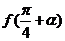 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com