
21.(本小题满分12分)
设数列{an}的前n项和为Sn,若{Sn}是首项为S1各项均为正数且公比为q的等比数列.
(Ⅰ)求数列{an}的通项公式an(用S1和q表示);
(Ⅱ)试比较an+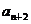 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
20.(本小题满分12分)
已知函数f(x)= x3-ax+b在y轴上截距为l,且曲线上一点P(
x3-ax+b在y轴上截距为l,且曲线上一点P( ,y0)处的切线斜率为
,y0)处的切线斜率为 ,求这一切线方程,并求该函数的极大值和极小值.
,求这一切线方程,并求该函数的极大值和极小值.
19.(本小题满分12分)
有6名2008年北京奥运志愿者,每人至少会英、法两种语言中的一种,其中5人会英语,4人会法语,现从6人中选派4人参加一项活动,需要2人能用英语交流,2人能用法语交流.
(Ⅰ)求两种语言都会的志愿者全部人选的概率;
(Ⅱ)求只会法语的志愿者人选的概率.
18.(本小题满分12分)
 如图:AE⊥平面ABCD,ABCD为正方形,
如图:AE⊥平面ABCD,ABCD为正方形,
AE=AB=2,F为BE中点.
(Ⅰ)求证:DE∥平面ACF;
(Ⅱ)求二面角B-AC-F的余弦值.
17.(本小题l0分)
在△ABC中,a、b、c分别是角A、B、C的对边,且 =-
=-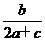 .
.
(Ⅰ)求角B的大小;
(Ⅱ)若b= ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.
16.表面积是100π的球(球心为O)与锐二面角的两个半平面分别切于点A、B,且△AOB的面积是10,则球心O到二面角的棱的距离是__________.
15.已知lgx+lgy=2,则 +
+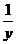 的最小值是_____________________.
的最小值是_____________________.
14.已知x、y满足约束条件 ,且z=-2x+y,则z的最小值是________.
,且z=-2x+y,则z的最小值是________.
13.现有甲种电脑56台,乙种电脑42台,如果用分层抽样的方法从中抽取一个容量为14的样本,则乙种电脑应抽样_____________台.
12.过点P(1,1)作曲线y=x3的两条切线l1、l2,设l1和l2的夹角为θ,则tanθ=( )
A. B.
B.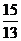 C.
C.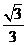 D.
D.
第Ⅱ卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com